Chapter 7 Push-forward, pooling and unpooling

This section shows how the push-forward operation of Definition 5.3 can be used to realize (un)pooling operations on CCs, and subsequently introduces (un)pooling operations for CCNNs. Further, this section demonstrates how CC-based pooling provides a unifying framework for image and graph-based pooling, and how shape-preserving pooling on CCs is related to the mapper on graphs.

In particular, we establish yet another unifying mathematical principle: pooling, as message passing, can be fundamentally built from push-forward operations. Thus, push-forward operations form the main fundamental building block from which all higher-order computations can be realized. This realization is important because it establishes a mathematical foundation for a unifying deep learning application programming interface (API) on complexes that combines pooling as well as message passing-based computations as a single operation. Indeed, in TopoModelX, one of our contributed Python packages, higher-order message passing and the pooling/unpooling operations are implemented as a single function across various topological domains.

7.1 CC-pooling and unpooling

We define a CC-based pooling operation that extends the main characteristics of image-based and graph-based pooling operations. Specifically, we build a pooling operation that `downscales’ the size of a signal supported on a CC \(\mbox{X}\). To this end, we exploit the hierarchical nature of CCs and define the pooling operation as a push-forward operation induced by a cochain map \(G\colon\mathcal{C}^{i}(\mathcal{X})\to \mathcal{C}^{j}(\mathcal{X})\) that pushes an \(i\)-cochain to a \(j\)-cochain. To obtain a useful pooling operation that downscales the size of its input \(i\)-cochain, we impose the constraint \(j>i\). Definition 7.1 realizes our idea of CC-pooling. Figure 7.1 visualizes the intuition behind Definition 7.1. In particular, Figure 7.1 shows an example of successive applications of pooling operations on cochains supported on a CC of dimension three.

Definition 7.1 (CC-pooling operation) Let \(\mbox{X}\) be a CC and \(G\colon\mathcal{C}^{i}( \mbox{X})\to \mathcal{C}^{j}( \mbox{X})\) a cochain map. The push-forward operation induced by \(G\) is called a CC-pooling operation if \(j>i\).

An example of successive CC-(un)pooling operations. A CC-pooling operation exploits the hierarchical structure of the underlying CC to coarsen a lower-rank cochain by pushing it forward to higher-order cells. CC-pooling operations improve invariance to certain distortions. Pink, blue, and green cells have ranks one, two, and three, respectively. A CC $\mbox{X}$ of dimension three is shown in (a). On $\mbox{X}$, we consider three cochain operators: $B_{0,1} \colon\mathcal{C}^1\to \mathcal{C}^0$, $B_{1,2} \colon\mathcal{C}^2\to \mathcal{C}^1$ and $B_{2,3}\colon\mathcal{C}^3\to \mathcal{C}^2$. For the top row in Figures (b), (c), and (d), we assume that we are initially given a 0-cochain $\mathbf{H}_0$, while for the bottom row in the same figure, we assume that we are initially given a 3-cochain $\mathbf{H}_3$. For instance, at the top row of Figure (b), the input 0-cochain $\mathbf{H}_0$ gets pushed forward via the functional $\mathcal{F}_{B_{0,1}^T} \colon\mathcal{C}^0\to \mathcal{C}^1$ to a 1-cochain $\mathbf{H}_1$. This push-forward operator induced by $B_{0,1}^T$ is a CC-pooling operator, since it sends a 0-cochain to a cochain of higher rank. At the bottom row of Figure (b), the push-forward operator $\mathcal{F}_{B_{0,1}}\colon \mathcal{C}^1\to \mathcal{C}^0$ induced by $B_{0,1}$ is an unpooling operator that sends a $1$-cochain to a $0$-cochain. Figures (c) and (d) are similar to (b), demonstrating the pooling operators induced by $B_{1,2}^T$ and $B_{2,3}^T$ (top), and the unpooling operators induced by $B_{1,2}$ and $B_{2,3}$ (bottom).

FIGURE 7.1: An example of successive CC-(un)pooling operations. A CC-pooling operation exploits the hierarchical structure of the underlying CC to coarsen a lower-rank cochain by pushing it forward to higher-order cells. CC-pooling operations improve invariance to certain distortions. Pink, blue, and green cells have ranks one, two, and three, respectively. A CC \(\mbox{X}\) of dimension three is shown in (a). On \(\mbox{X}\), we consider three cochain operators: \(B_{0,1} \colon\mathcal{C}^1\to \mathcal{C}^0\), \(B_{1,2} \colon\mathcal{C}^2\to \mathcal{C}^1\) and \(B_{2,3}\colon\mathcal{C}^3\to \mathcal{C}^2\). For the top row in Figures (b), (c), and (d), we assume that we are initially given a 0-cochain \(\mathbf{H}_0\), while for the bottom row in the same figure, we assume that we are initially given a 3-cochain \(\mathbf{H}_3\). For instance, at the top row of Figure (b), the input 0-cochain \(\mathbf{H}_0\) gets pushed forward via the functional \(\mathcal{F}_{B_{0,1}^T} \colon\mathcal{C}^0\to \mathcal{C}^1\) to a 1-cochain \(\mathbf{H}_1\). This push-forward operator induced by \(B_{0,1}^T\) is a CC-pooling operator, since it sends a 0-cochain to a cochain of higher rank. At the bottom row of Figure (b), the push-forward operator \(\mathcal{F}_{B_{0,1}}\colon \mathcal{C}^1\to \mathcal{C}^0\) induced by \(B_{0,1}\) is an unpooling operator that sends a \(1\)-cochain to a \(0\)-cochain. Figures (c) and (d) are similar to (b), demonstrating the pooling operators induced by \(B_{1,2}^T\) and \(B_{2,3}^T\) (top), and the unpooling operators induced by \(B_{1,2}\) and \(B_{2,3}\) (bottom).

In Definition 7.2, we introduce an unpooling operation on CCs that pushes forward a cochain to a lower-rank cochain. Figure 7.1 shows as example of unpooling on CCs.

Definition 7.2 (CC-unpooling operation) Let \(\mbox{X}\) be a CC and \(G\colon\mathcal{C}^i( \mbox{X})\to \mathcal{C}^j( \mbox{X})\) a cochain map. The push-forward operation induced by \(G\) is called a CC-unpooling operation if \(j<i\).

7.2 Formulating common pooling operations as CC-pooling

In this section, we formulate common pooling operations in terms of CC-pooling. In particular, we demonstrate that graph and image pooling can be cast as CC-pooling.

7.2.1 Graph pooling as CC-pooling

Here, we briefly demonstrate that the CC-pooling operation (Definition 7.1) is consistent with a graph-based pooling algorithm. Let \(\mathbf{H}_0\) be a cochain defined on the vertices and edges of a graph \(\mathcal{G}\). Moreover, let \(\mathbf{H}^{\prime}_0\) be a cochain defined on the vertices of a coarsened version \(\mathcal{G}^{\prime }\) of \(\mathcal{G}\). Under such a setup, \(\mathbf{H}^{\prime}_0\) represents a coarsened version of \(\mathbf{H}_0\). A graph pooling function supported on the pair \((\mathcal{G},\mathbf{H}_0)\) is a function of the form \(\mathcal{POOL} \colon (\mathcal{G},\mathbf{H}_0) \to (\mathcal{G}^{\prime},\mathbf{H}^{\prime}_0)\) that sends every vertex in \(\mathcal{G}\) to a vertex in \(\mathcal{G}^{\prime}\), which corresponds to a cluster of vertices in \(\mathcal{G}\). We now elucidate how the function \(\mathcal{POOL}\) can be realized in terms of CC-pooling.

Proposition 7.1 (The role of CC-pooling) The function \(\mathcal{POOL}\) can be realized in terms of CC-pooling operations.

Proof. Each vertex in the graph \(\mathcal{G}^{\prime}\) represents a cluster of vertices in the original graph \(\mathcal{G}\). Using the membership of these clusters, we construct a CC by augmenting \(\mathcal{G}\) by a collection of 2-cells, so that each of these cells corresponds to a supernode of \(\mathcal{G}^{\prime}\). We denote the resulting CC structure by \(\mathcal{X}_{\mathcal{G}}\), consisting of \(\mathcal{G}\) augmented by the 2-cells. Hence, any 0-cochain \(\mathbf{H}^{\prime}_0\) defined on \(\mathcal{G}^{\prime}\) can be written as a 2-cochain \(\mathbf{H}_2 \in \mathcal{C}^2(\mathcal{X}_{\mathcal{G}})\). The relation between the vertices of the original graph \(\mathcal{G}\) and the vertices of the pooled graph \(\mathcal{G}^{\prime}\), or equivalently the CC \(\mathcal{X}_{\mathcal{G}}\), is described via the incidence matrix \(B_{0,2}^T\). Hence, learning the signal \(\mathbf{H}_2\) can be realized in terms of a map \(B_{0,2}^T \colon \mathcal{C}^{2} (\mathcal{X}_{\mathcal{G}}) \to \mathcal{C}^{0}(\mathcal{X}_{\mathcal{G}})\) that pushes forward the cochain \(\mathbf{H}_0\) to \(\mathbf{H}_2\).

The 2-cells defined on \(\mathcal{X}_{\mathcal{G}}\) can be practically constructed using the mapper on graphs (Hajij, Wang, and Rosen 2018), a classification tool in TDA. See Section 7.4 for more details of such a construction.

7.2.2 Image pooling as CC-pooling

Since images can be realized as lattice graphs, a signal stored on an image grid can be realized as a 0-cochain of the lattice graph that corresponds to the image. See Figures 7.2(a–b) for an example. Here, we demonstrate that the CC-pooling operation (Definition 7.1) is consistent with the known image-pooling definition. Indeed, one may augment the lattice graph of Figure 7.2(b) by 2-cells, as shown in Figure 7.2(c), to perform the image pooling operation. Usually, these cells have a regular window size. In Figure 7.2(c), we have chosen the pooling window size, or equivalently the size of the 2-cell, to be \(2\times 2\), and the pooling stride to be 1. The image pooling operation in this case can be realized as a CC-pooling operation induced by the cochain map \(B_{0,2}^T \colon\mathcal{C}^0 \to \mathcal{C}^2\), as visualized in Figure 7.2(d). We formally record this in the following proposition.

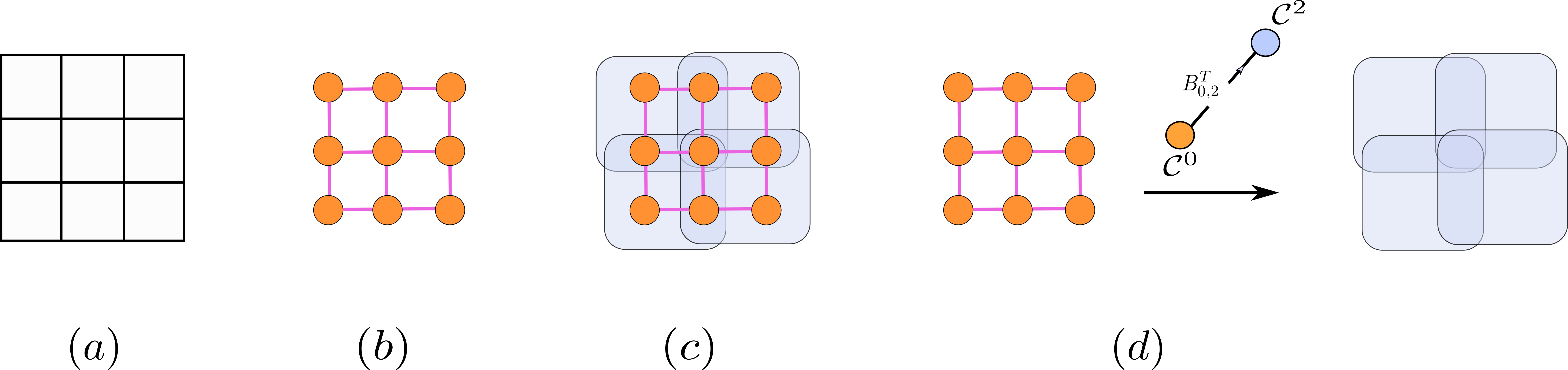
Realizing image pooling in terms of CC-pooling. (a): An image of size $3\times3$. (b): The lattice graph that corresponds to the image given in (a). (c): Augmenting the lattice graph with 2-cells. Choosing these particular cells shown in (c) is equivalent to choosing the image-pooling window size to be $2\times 2$ and the pooling stride to be one. (d): Performing the image-pooling computation is equivalent to performing a CC-pooling operation induced by the cochain map $B_{0,2}^T \colon\mathcal{C}^0 \to \mathcal{C}^2$, which pushes forward the image signal (the $0$-cochain supported on $\mathcal{X}^2$) to a signal supported on $\mathcal{X}^2$.

FIGURE 7.2: Realizing image pooling in terms of CC-pooling. (a): An image of size \(3\times3\). (b): The lattice graph that corresponds to the image given in (a). (c): Augmenting the lattice graph with 2-cells. Choosing these particular cells shown in (c) is equivalent to choosing the image-pooling window size to be \(2\times 2\) and the pooling stride to be one. (d): Performing the image-pooling computation is equivalent to performing a CC-pooling operation induced by the cochain map \(B_{0,2}^T \colon\mathcal{C}^0 \to \mathcal{C}^2\), which pushes forward the image signal (the \(0\)-cochain supported on \(\mathcal{X}^2\)) to a signal supported on \(\mathcal{X}^2\).

Proposition 7.2 (Realization of image pooling) An image pooling operator can be realized in terms of a push-forward operator from the underlying image domain to a 2-dimensional CC obtained by augmenting the image by appropriate 2-cells where image pooling computations occur.

Proof. The proof is a straightforward conclusion from the definition of image pooling.

7.3 Pooling and unpooling CCNNs

The pooling operator of Definition 7.1 considers only the special case in which the tensor diagram of a CCNN has a single edge. In what follows, we generalize the notion of pooling by identifying the defining properties that characterize a CCNN as a pooling CCNN. To this end, we start with a CCNN whose tensor diagram has a height of one.

Definition 7.3 (Pooling CCNN of height one) Consider a CCNN represented by a tensor diagram \(\mbox{CCNN}_{\mathbf{G};\mathbf{W}}\) of height one. Let \(\mathcal{C}^{i_1}\times\mathcal{C}^{i_2}\times \cdots \times \mathcal{C}^{i_m}\) be the domain and let \(\mathcal{C}^{j_1}\times\mathcal{C}^{j_2}\times \cdots \times \mathcal{C}^{j_n}\) be the codomain of the CCNN. Let \(i_{min}=min(i_1,\ldots,i_m)\) and \(j_{min}=min(j_1,\ldots,j_n)\). We say that the CCNN is a pooling CCNN of height one if

  1. \(i_{min}< j_{min}\), and
  2. the tensor diagram \(\mbox{CCNN}_{\mathbf{G};\mathbf{W}}\) has an edge labeled by a cochain operator \(G\colon \mathcal{C}^{i_{min}} \to \mathcal{C}^{k}\) for some \(k\geq j_{min}\).

Intuitively, a CCNN represented by a tensor diagram of height one is a pooling CCNN of height one if it pushes forward its lowest-rank signals to higher-rank cells. Observe that a readout operation can be realized as a pooling CCNN of height one; see Figure 7.3 for an illustration.

Examples of pooling operations. In this example, a CC of dimension three is displayed. A rank cell of rank $3$ (shown in green) has the highest rank among all cells in the CC. (a): A pooling CCNN of height one pools a cochain vector $(\mathbf{H}_0,\mathbf{H}_1)$ to a 2-cochain $\mathbf{H}_2$. (b): A readout operation can be realized as a pooling CCNN of height one by encapsulating the entire CC by a single (green) cell of rank higher than all other cells in the CC, and by pooling (reading out) all signals of lower-order cells to the encapsulating (green) cell.

FIGURE 7.3: Examples of pooling operations. In this example, a CC of dimension three is displayed. A rank cell of rank \(3\) (shown in green) has the highest rank among all cells in the CC. (a): A pooling CCNN of height one pools a cochain vector \((\mathbf{H}_0,\mathbf{H}_1)\) to a 2-cochain \(\mathbf{H}_2\). (b): A readout operation can be realized as a pooling CCNN of height one by encapsulating the entire CC by a single (green) cell of rank higher than all other cells in the CC, and by pooling (reading out) all signals of lower-order cells to the encapsulating (green) cell.

A CCNN may not perform a pooling operation at every layer, and it may preserve the dimensionality of the lowest-rank signal. Before we give the general definition of pooling CCNNs, we first define lowest rank-preserving CCNNs of height one.

Definition 7.4 (Lowest rank-preserving CCNN of height one) Consider a CCNN represented by a tensor diagram of height one. Let \(\mathcal{C}^{i_1}\times\mathcal{C}^{i_2}\times \cdots \times \mathcal{C}^{i_m}\) be the domain and let \(\mathcal{C}^{j_1}\times\mathcal{C}^{j_2}\times \cdots \times \mathcal{C}^{j_n}\) be the codomain of the CCNN. Let \(i_{min}=min(i_1,\ldots,i_m)\) and \(j_{min}=min(j_1,\ldots,i_n)\). We say that the CCNN is a lowest rank-preserving CCNN of height one if \(i_{min}= j_{min}\).

Every CCNN is a composition of CCNNs that are represented by tensor diagrams of height one. Hence, pooling CCNNs can be characterized in terms of tensor diagrams of height one, as elaborated in Definition 7.5.

Definition 7.5 (Pooling CCNN) Let \(\mbox{CCNN}_{\mathbf{G};\mathbf{W}}\) be a tensor diagram representation of a CCNN. We decompose the CCNN as \[\begin{equation*} \mbox{CCNN}_{\mathbf{G};\mathbf{W}}= \mbox{CCNN}_{\mathbf{G}_N;\mathbf{W}_N} \circ \cdots \circ \mbox{CCNN}_{\mathbf{G}_1;\mathbf{W}_1}, \end{equation*}\] where \(\mbox{CCNN}_{\mathbf{G}_i;\mathbf{W}_i},i=1,\ldots,N\), is a tensor diagram of height one representing the \(i\)-th layer of the CCNN, and \(\mathbf{G}_i \subseteq \mathbf{G}\). We call the CCNN represented by \(\mbox{CCNN}_{\mathbf{G};\mathbf{W}}\) a pooling CCNN if

  1. every \(\mbox{CCNN}_{\mathbf{G}_i;\mathbf{W}_i}\) is either a pooling CCNN of height one or a lowest rank-preserving CCNN of height one, and
  2. at least one of the layers \(\mbox{CCNN}_{\mathbf{G}_i;\mathbf{W}_i}\) is a pooling CCNN of height one. \end{enumerate}

Intuitively, a pooling CCNN is a CCNN whose tensor diagram forms a ‘ladder’ that pushes signals to higher-rank cells at every layer. Figure 5.4(d) gives an example of a pooling CCNN of height two.

An unpooling CCNN of height one is defined similarly to a pooling CCNN of height one (Definition 7.3), with the only difference being that the inequality \(i_{min}<j_{min}\) becomes \(i_{min}>j_{min}\). Moreover, an unpooling CCNN (Definition 7.6) is defined analogously to a pooling CCNN (Definition 7.5).

Definition 7.6 (Unpooling CCNN) Let \(\mbox{CCNN}_{\mathbf{G};\mathbf{W}}\) be a tensor diagram representation of a CCNN. We decompose the CCNN as \[\begin{equation*} \mbox{CCNN}_{\mathbf{G};\mathbf{W}}= \mbox{CCNN}_{\mathbf{G}_N;\mathbf{W}_N} \circ \cdots \circ \mbox{CCNN}_{\mathbf{G}_1;\mathbf{W}_1}, \end{equation*}\] where \(\mbox{CCNN}_{\mathbf{G}_i;\mathbf{W}_i},i=1,\ldots,N\), is a tensor diagram of height one representing the \(i\)-th layer of the CCNN, and \(\mathbf{G}_i \subseteq \mathbf{G}\). We call the CCNN represented by \(\mbox{CCNN}_{\mathbf{G};\mathbf{W}}\) an unpooling CCNN if

  1. every \(\mbox{CCNN}_{\mathbf{G}_i;\mathbf{W}_i}\) is either an unpooling CCNN of height one or a lowest rank-preserving CCNN of height one, and
  2. at least one of the layers \(\mbox{CCNN}_{\mathbf{G}_i;\mathbf{W}_i}\) is an unpooling CCNN of height one.

7.4 Mapper and the CC-pooling operation

In practice, constructing a useful CC-pooling operation on a higher-order domain is determined by the higher-rank cells in the input CC. Similar to image-based models, CC-pooling operations can be applied sequentially at the end of a higher-order network to provide a summary representation of the input domain; see Figure 7.1 for an example. Such a hierarchical summary might not be readily available in the input CC. For instance, if \(\mathcal{X}\) is a graph, then a CC-pooling operation, as given in Definition 7.1, can only push forward an input node-signal to an edge-signal, which may not always provide a compact summary of the input signal.

In such situations, one may choose to augment the input CC \(\mathcal{X}\) with a collection of new cells of dimension \(\dim(\mathcal{X})+1\) so that the new cells approximate the shape of the input CC \(\mathcal{X}\). Figure 7.4 displays an example of augmenting a graph \(\mathcal{X}\), which is a CC of dimension one, with new cells of dimension two using the mapper on graphs (MOG) construction suggested in (Dey, Mémoli, and Wang 2016; Singh et al. 2007; Hajij, Wang, and Rosen 2018)6. The augmented higher-rank cells obtained from the MOG construction summarize the shape features of the underlying graph, which is a desirable pooling characteristic (e.g., in shape analysis). We refer to Appendix E for details about the MOG construction of topology-preserving CC-pooling operations.

An example of constructing a shape-preserving pooling operation on a CC $\mathcal{X}$. Here, we demonstrate the case in which $\mathcal{X}$ is a graph. We utilize the *mapper on graphs (MOG)* construction [@singh2007topological; @hajij2018mog], a graph skeletonization algorithm that can be used to augment $\mathcal{X}$ with topology-preserving cells of rank $2$. (a): An input graph $\mathcal{X}$, which is a CC of dimension one. (b): The MOG algorithm receives three elements as input, namely the graph $\mathcal{X}$, a feature-preserving scalar function $g\colon\mathcal{X}^0\to [a,b]$, and a cover $\mathcal{U}$ of range $[a,b]$, that is a collection of open sets that covers the closed interval $[a,b]$. The scalar function $g$ is used to pull back a covering $\mathcal{U}$ on the range $[a,b]$ to a covering on $\mathcal{X}$. The colors of nodes in Figure (b) indicate the scalar values of $g$. In Figure (b), $\mathcal{X}$ is split into four segments so that each segment corresponds to a cover element of $\mathcal{U}$. (c): The figure shows the connected components in pull-back cover elements. Each connected component is enclosed by a blue cell. Each of these blue cells is considered as a cell of rank $2$. We augment $\mathcal{X}$ with the blue cells to form a CC of dimension two, consisting of the original 0-cells and 1-cells in $\mathcal{X}$ as well as the augmented 2-cells. This augmented CC is denoted by $\mathcal{X}_{g,\mathcal{U}}$. (d): The MOG algorithm constructs a graph, whose nodes are the connected components contained in each cover element in the pull-back of the cover $\mathcal{U}$, and whose edges are formed by the intersection between these connected components. In other words, the MOG-generated graph summarizes the connectivity between the augmented cells of rank $2$ added via the MOG algorithm. Observe that the adjacency matrix of the MOG-generated graph given in Figure (d) is equivalent to the adjacency matrix $A_{2,2}$ of $\mathcal{X}_{g,\mathcal{U}}$, since 2-cells in $\mathcal{X}$ are 2-adjacent if and only if they intersect on a node (and the latter occurs if and only if there is an edge between the nodes of the MOG-generated graph). Given this CC structure, the cochain map $B_{0,2}^T\colon\mathcal{C}^0(X_{g,\mathcal{U}})\to \mathcal{C}^2(X_{g,\mathcal{U}})$ can be used to induce a shape-preserving CC-pooling operation. Moreover, a signal $\mathbf{H}_0$ supported on the nodes of $\mathcal{X}$ can be push-forwarded and pooled to a signal $\mathbf{H}_2$ supported on the augmented 2-cells. This figure is inspired from [@hajij2018mog].

FIGURE 7.4: An example of constructing a shape-preserving pooling operation on a CC \(\mathcal{X}\). Here, we demonstrate the case in which \(\mathcal{X}\) is a graph. We utilize the mapper on graphs (MOG) construction (Singh et al. 2007; Hajij, Wang, and Rosen 2018), a graph skeletonization algorithm that can be used to augment \(\mathcal{X}\) with topology-preserving cells of rank \(2\). (a): An input graph \(\mathcal{X}\), which is a CC of dimension one. (b): The MOG algorithm receives three elements as input, namely the graph \(\mathcal{X}\), a feature-preserving scalar function \(g\colon\mathcal{X}^0\to [a,b]\), and a cover \(\mathcal{U}\) of range \([a,b]\), that is a collection of open sets that covers the closed interval \([a,b]\). The scalar function \(g\) is used to pull back a covering \(\mathcal{U}\) on the range \([a,b]\) to a covering on \(\mathcal{X}\). The colors of nodes in Figure (b) indicate the scalar values of \(g\). In Figure (b), \(\mathcal{X}\) is split into four segments so that each segment corresponds to a cover element of \(\mathcal{U}\). (c): The figure shows the connected components in pull-back cover elements. Each connected component is enclosed by a blue cell. Each of these blue cells is considered as a cell of rank \(2\). We augment \(\mathcal{X}\) with the blue cells to form a CC of dimension two, consisting of the original 0-cells and 1-cells in \(\mathcal{X}\) as well as the augmented 2-cells. This augmented CC is denoted by \(\mathcal{X}_{g,\mathcal{U}}\). (d): The MOG algorithm constructs a graph, whose nodes are the connected components contained in each cover element in the pull-back of the cover \(\mathcal{U}\), and whose edges are formed by the intersection between these connected components. In other words, the MOG-generated graph summarizes the connectivity between the augmented cells of rank \(2\) added via the MOG algorithm. Observe that the adjacency matrix of the MOG-generated graph given in Figure (d) is equivalent to the adjacency matrix \(A_{2,2}\) of \(\mathcal{X}_{g,\mathcal{U}}\), since 2-cells in \(\mathcal{X}\) are 2-adjacent if and only if they intersect on a node (and the latter occurs if and only if there is an edge between the nodes of the MOG-generated graph). Given this CC structure, the cochain map \(B_{0,2}^T\colon\mathcal{C}^0(X_{g,\mathcal{U}})\to \mathcal{C}^2(X_{g,\mathcal{U}})\) can be used to induce a shape-preserving CC-pooling operation. Moreover, a signal \(\mathbf{H}_0\) supported on the nodes of \(\mathcal{X}\) can be push-forwarded and pooled to a signal \(\mathbf{H}_2\) supported on the augmented 2-cells. This figure is inspired from (Hajij, Wang, and Rosen 2018).

References

Dey, Tamal K., Facundo Mémoli, and Yusu Wang. 2016. “Multiscale Mapper: Topological Summarization via Codomain Covers.” In Proceedings of the Twenty-Seventh Annual ACM-SIAM Symposium on Discrete Algorithms, 997–1013. SIAM.
Hajij, Mustafa, Bei Wang, and Paul Rosen. 2018. “MOG: Mapper on Graphs for Relationship Preserving Clustering.” arXiv Preprint arXiv:1804.11242.
Singh, Gurjeet, Facundo Mémoli, Gunnar E Carlsson, et al. 2007. “Topological Methods for the Analysis of High Dimensional Data Sets and 3d Object Recognition.” PBG@ Eurographics 2: 091–100.

  1. While graph skeletonization using the mapper algorithm (Singh et al. 2007) has been studied in (Dey, Mémoli, and Wang 2016), our implementation and discussion here relies on the notions suggested in (Hajij, Wang, and Rosen 2018).↩︎