C CCNN architecture search and topological quantum field theories
The problem of CCNN architecture search for a given TDL task can be cast as a hyperparameter optimization problem over the space of CCNNs. More precisely, consider the query of searching for an optimal CCNN between two fixed Cartesian products \(\mathcal{C}^{i_1}\times\mathcal{C}^{i_2}\times \ldots \times \mathcal{C}^{i_m}\) and \(\mathcal{C}^{j_1}\times\mathcal{C}^{j_2}\times \ldots \times \mathcal{C}^{j_n}\) of cochain spaces. In practice, this query poses a challenging problem. Rather than performing a computationally expensive CCNN search directly, an alternative approach is to conduct a search in the simpler space of marked trivalent graphs between marked points \(\{i_1,\ldots,i_m\}\) and \(\{j_1,\ldots,j_n\}\), and then map the resulting marked trivalent graph to a corresponding CCNN architecture. In the present section, we briefly sketch such a graph-based search method using tools from topological quantum field theory (TQFT) (Turaev 2016), and accordingly we assume some familiarity with the basics of category theory.
Tensor diagrams draw their inspiration from TQFT, in which arbitrary maps between topological spaces are constructed from simpler and more manageable building blocks. The main workflow in TQFT constructions involves breaking down the topological spaces under consideration into simpler subspaces, and subsequently utilizing maps between the subspaces to construct maps between the initial topological spaces; see Figure C.1(a). Thus, the topological properties of maps between topological spaces are better understood via the topological properties of simpler constituent maps between respective subspaces. This can be especially useful in applications such as knot theory or the study of three-dimensional manifolds, where understanding the topological properties of involved maps is the main interest (Turaev 2016).
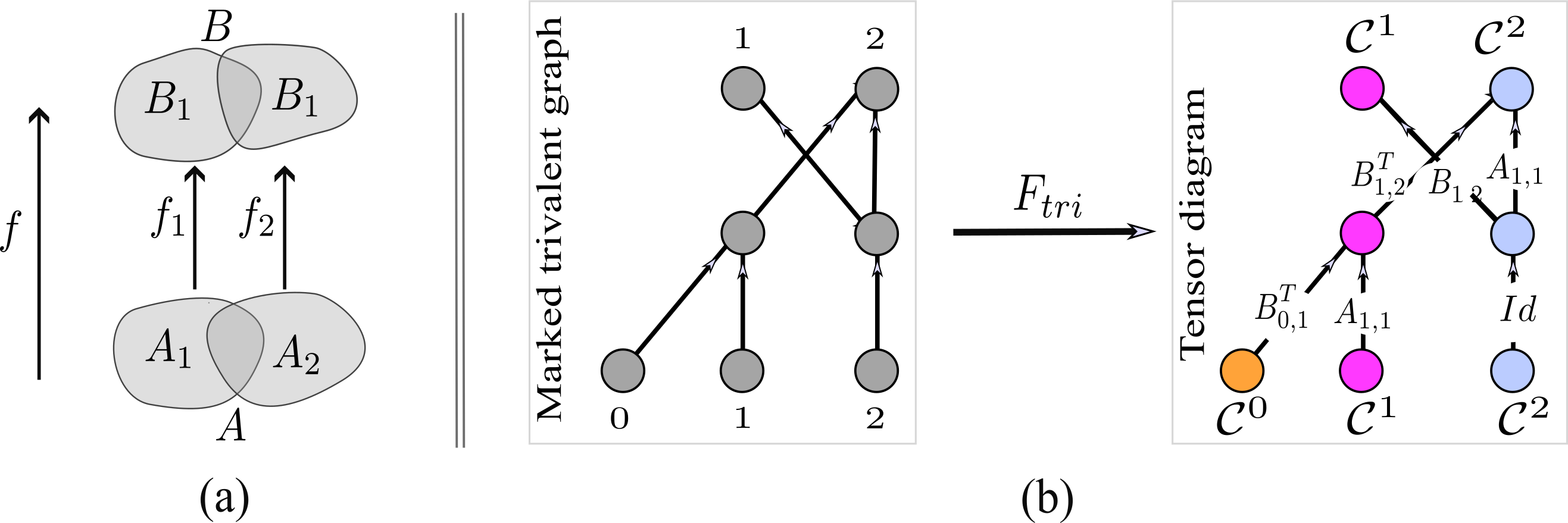
FIGURE C.1: A sketch of the main idea of a TQFT construction in (a) and a functor \(F_{tri}\) for constructing tensor diagrams in (b). (a): In the depicted example, the goal is to construct a map \(f\colon A\to B\) between two topological spaces \(A\) and \(B\). We first decompose \(A\) and \(B\) into simpler sub-spaces, say \(A = A_1 \cup A_2\) and \(B = B_1 \cup B_2\), so that \({A_1,A_2}\) and \({B_1,B_2}\) are `more elementary spaces’ than \(A\) and \(B\), respectively. We then construct two maps \(f_1 \colon A_1 \to B_1\) and \(f_2 \colon A_2 \to B_2\), and use them to construct \(f\). (b): A visual example of a functor \(F_{tri}\) that pairs each marked trivalent graph with a corresponding tensor diagram. This example sends a marked trivalent graph with marked points \(\{0,1,2\}\) at the bottom and marked points \(\{1,2\}\) at the top to a tensor diagram with domain \(\mathcal{C}^{0} \times \mathcal{C}^{1}\times \mathcal{C}^{2}\) and codomain \(\mathcal{C}^{1}\times \mathcal{C}^{2}\). Once the push-forward, the merge and the split nodes are defined, the functor \(F_{tri}\) attaches a well-defined tensor diagram to each trivalent graph. A CCNN can be then constructed from the tensor diagram.
Before we introduce the relation between tensor diagrams and TQFTs, we sketch two required preliminaries, namely marked trivalent graphs and TQFTs. First, we define the objects and morphisms of the category of marked trivalent graphs \(Tri\). A marked trivalent graph is intuitively described via its layout. Consider the 2d-disk \([0,1]\times [0,1]\) with a collection of marked points \(\{i_1,\ldots,i_m\}\) at the bottom and a collection of marked points \(\{j_1,\ldots,j_n\}\) at the top. A marked trivalent graph is a graph that is drawn inside the disk in such a way that all edges flow within the disk, connecting the marked points at the top with the marked points at the bottom, and meeting at each vertex with exactly three edges. In the category \(Tri\), a trivalent graph with marked points \(\{i_1,\ldots,i_m\}\) and \(\{j_1,\ldots,j_n\}\) at the bottom and top, respectively, plays the role of a morphism between the object \(\{i_1,\ldots,i_m\}\) and the object \(\{j_1,\ldots,j_n\}\). The composition of two such morphisms, when admissible, is defined to be the vertical concatenation of their corresponding marked trivalent graphs. The vertical concatenation of marked trivalent graphs yields a marked trivalent graph. Finally, any trivalent graph can be built by concatenating horizontally and vertically three elementary trivalent graphs similar to the graph shown in Figure C.1(b), ignoring the labels in the figure.
At a high level, a TQFT is a functor \(F\colon Bord_{n}\to Vec_{K}\) that assigns a \(K\)-vector space \(F(x)\in Vec_{K}\) to each \(n\)-manifold \(x \in Bord_{n}\), and a linear map \(F(f)\) to each \((n+1)\)-cobordism \(f \in Bord_{n}\). It is noted that a \((n+1)\)-cobordism is an \((n+1)\)-manifold representing a morphism between two \(n\)-manifolds. The functor \(F\) is typically defined on a few elementary morphisms in \(Bord_{n}\), but can be extended to arbitrary morphisms in \(Bord_{n}\) by preserving the structure of the elementary maps when mapped via \(F\). Such a functor enables the study of \(n\)-manifolds and \((n+1)\)-cobordisms defined between them by mapping \(n\)-manifolds to their corresponding simpler vector spaces in \(Vec_{K}\) and by mapping \((n+1)\)-cobordisms to linear maps between the corresponding vector spaces.
To establish the relation between marked trivalent graphs and tensor diagrams, we introduce a new TQFT \(F_{tri}\) that sends each morphism (marked trivalent graph) in \(Tri\) to a corresponding tensor diagram by labeling marked trivalent graphs with appropriate cochain maps. Figure C.1(b) shows an illustration of such a functor \(F_{tri}\). Through the lens of \(F_{tri}\), the relation between tensor diagrams and marked trivalent graphs becomes clear; a tensor diagram is a marked trivalent graph whose edges are labeled via cochain maps. The functor \(F_{tri}\) allows us to search the space of marked trivalent graphs as an equivalent way of conducting CCNN architecture search, since CCNNs are represented by tensor diagrams.