Chapter 6 Message passing
In this section, we explain the relation between the notion of the merge node introduced in Section 5.2 and higher-order message passing. In particular, we prove that higher-order message passing on CCs can be realized in terms of the elementary tensor operations introduced in Section 5.3. Further, we demonstrate the connection between CCANNs (Section 5.5) and higher-order message passing, and introduce an attention version of higher-order message passing. We first define higher-order message passing on CCs, generalizing notions introduced in (Hajij, Istvan, and Zamzmi 2020).
We remark that many of the constructions discussed here are presented in their most basic form, but can be extended further. An important aspect in this direction is the construction of message-passing protocols that are invariant or equivariant with respect to the action of a specific group.
6.1 Definition of higher-order message passing
Higher-order message passing refers to a computational framework that involves exchanging messages among entities and cells in a higher-order domain using a set of neighborhood functions. In Definition 6.1, we formalize the notion of higher-order message passing for CCs. Figure 6.1 illustrates Definition 6.1.
Definition 6.1 (Higher-order message passing on a CC) Let \(\mathcal{X}\) be a CC. Let \(\mathcal{N}=\{ \mathcal{N}_1,\ldots,\mathcal{N}_n\}\) be a set of neighborhood functions defined on \(\mathcal{X}\). Let \(x\) be a cell and \(y\in \mathcal{N}_k(x)\) for some \(\mathcal{N}_k \in \mathcal{N}\). A message \(m_{x,y}\) between cells \(x\) and \(y\) is a computation that depends on these two cells or on the data supported on them. Denote by \(\mathcal{N}(x)\) the multi-set \(\{\!\!\{ \mathcal{N}_1(x) , \ldots , \mathcal{N}_n (x) \}\!\!\}\), and by \(\mathbf{h}_x^{(l)}\) some data supported on the cell \(x\) at layer \(l\). Higher-order message passing on \(\mathcal{X}\), induced by \(\mathcal{N}\), is defined via the following four update rules: \[\begin{align} m_{x,y} &= \alpha_{\mathcal{N}_k}(\mathbf{h}_x^{(l)},\mathbf{h}_y^{(l)}), \tag{6.1} \\ m_{x}^k &= \bigoplus_{y \in \mathcal{N}_k(x)} m_{x,y}, \; 1\leq k \leq n, \tag{6.2} \\ m_{x} &= \bigotimes_{ \mathcal{N}_k \in \mathcal{N} } m_x^k, \tag{6.3} \\ \mathbf{h}_x^{(l+1)} &= \beta (\mathbf{h}_x^{(l)}, m_x). \tag{6.4} \end{align}\] Here, \(\bigoplus\) is a permutation-invariant aggregation function called the intra-neighborhood of \(x\), \(\bigotimes\) is an aggregation function called the inter-neighborhood of \(x\), and \(\alpha_{\mathcal{N}_k},\beta\) are differentiable functions.
FIGURE 6.1: An illustration of higher-order message passing. Left-hand side: a collection of neighborhood functions \(\mathcal{N}_1,\ldots,\mathcal{N}_k\) are selected. The selection typically depends on the learning task. Right-hand side: for each \(\mathcal{N}_k\), the messages are aggregated using an intra-neighborhood function \(\bigoplus\). The inter-neighborhood function \(\bigotimes\) aggregates the final messages obtained from all neighborhoods.
Some remarks on Definition 6.1 are as follows. First, the message \(m_{x,y}\) in Equation (6.1) does not depend only on the data \(\mathbf{h}_x^{(l)}\), \(\mathbf{h}_y^{(l)}\) supported on the cells \(x, y\); it also depends on the cells themselves. For instance, if \(\mathcal{X}\) is a cell complex, the orientation of both \(x\) and \(y\) factors into the computation of message \(m_{x,y}\). Alternatively, \(x\cup y\) or \(x\cap y\) might be cells in \(\mathcal{X}\) and it might be useful to include their data in the computation of message \(m_{x,y}\). This unique characteristic only manifests in higher-order domains, and does not occur in graphs-based message-passing frameworks (Gilmer et al. 2017; Bronstein et al. 2021)4. Second, higher-order message passing relies on the choice of a set \(\mathcal{N}\) of neighborhood functions. This is also a unique characteristic that only occurs in a higher-order domain, where a neighborhood function is necessarily described by a set of neighborhood relations rather than graph adjacency as in graph-based message passing. Third, in Equation (6.1), since \(y\) is implicitly defined with respect to a neighborhood relation \(\mathcal{N}_k \in \mathcal{N},\) the function \(\alpha_{\mathcal{N}_k}\) and the message \(m_{x,y}\) depend on \(\mathcal{N}_k\). Fourth, the inter-neighborhood \(\bigotimes\) does not necessarily have to be a permutation-invariant aggregation function. For instance, it is possible to set an order on the multi-set \(\mathcal{N}(x)\) and compute \(m_x\) with respect to this order. Finally, higher-order message passing relies on two aggregation functions, the intra-neighborhood and inter-neighborhood, whereas graph-based message passing relies on a single aggregation function. The choice of set \(\mathcal{N}\), as illustrated in Chapter 4, enables the use of a variety of neighborhood functions in higher-order message passing.
Remark. The push-forward operator given in Definition 5.3 is related to the update rule of Equation (6.1). On one hand, Equation (6.1) requires two cochains \(\mathbf{X}_i= [\mathbf{h}_{x^i_1}^{(l)},\ldots,\mathbf{h}_{x^i_{|\mathcal{X}^i|}}^{(l)}]\) and \(\mathbf{Y}_{j}^{(l)}=[\mathbf{h}_{y^{j}_1}^{(l)},\ldots,\mathbf{h}_{y^{j}_{|\mathcal{X}^{j}|}}^{(l)}]\) to compute \(\mathbf{X}^{(l+1)}_i = [\mathbf{h}_{x^i_1}^{(l+1)},\ldots,\mathbf{h}_{x^i_{|\mathcal{X}^i|}}^{(l+1)}]\), so signals on both \(\mathcal{C}^j\) and \(\mathcal{C}^i\) must be present in order to execute Equation (6.1). From this perspective, it is natural and customary to think about this operation as an update rule. On the other hand, the push-forward operator of Definition 5.3 computes a cochain \(\mathbf{K}_{j} \in \mathcal{C}^j\) given a cochain \(\mathbf{H}_i\in \mathcal{C}^i\). As a single cochain \(\mathbf{H}_i\) is required to perform this computation, it is natural to think about Equation (5.2) as a function. See Section 6.3 for more details.
The higher-order message-passing framework given in Definition 6.1 can be used to construct novel neural network architectures on a CC, as we have also alluded in Figure 5.2. First, a CC \(\mathcal{X}\) and cochains \(\mathbf{H}_{i_1}\ldots, \mathbf{H}_{i_m}\) supported on \(\mathcal{X}\) are given. Second, a collection of neighborhood functions are chosen, taking into account the desired learning task. Third, the update rules of Definition 6.1 are executed on the input cochains \(\mathbf{H}_{i_1}\ldots, \mathbf{H}_{i_m}\) using the chosen neighborhood functions. The second and the third steps are repeated to obtain the final computations.
Definition 6.2 (Higher-order message-passing neural network) We refer to to any neural network constructed using Definition 6.1 as a higher-order message-passing neural network.
6.2 Higher-order message-passing neural networks are CCNNs
In this section, we show that higher-order message-passing computations can be realized in terms of merge node computations, and therefore that higher-order message-passing neural networks are CCNNs. As a consequence, higher-order message passing unifies message passing on simplicial complexes, cell complexes and hypergraphs through a coherent set of update rules and, alternatively, through the expressive language of tensor diagrams.
Theorem 6.1 (Merge node computation) The higher-order message-passing computations of Definition 6.1 can be realized in terms of merge node computations.
Proof. Let \(\mathcal{X}\) be a CC. Let \(\mathcal{N}=\{ \mathcal{N}_1,\ldots,\mathcal{N}_n\}\) be a set of neighborhood functions as specified in Definition 6.1. Let \(G_k\) be the matrix induced by the neighborhood function \(\mathcal{N}_k\). We assume that the cell \(x\) given in Definition 6.1 is a \(j\)-cell and the neighbors \(y \in \mathcal{N}_k(x)\) are \(i_k\)-cells. We will show that Equations (6.1)–(6.4) can be realized as applications of merge nodes. In what follows, we define the neighborhood function to be \(\mathcal{N}_{Id}(x)=\{x\}\) for \(x\in \mathcal{X}\). Moreover, we denote the associated neighborhood matrix of \(\mathcal{N}_{Id}\) by \(Id\colon\mathcal{C}^j\to \mathcal{C}^j\), as it is the identity matrix.
Computing message \(m_{x,y}\) of Equation (6.1) involves two cochains: \[\begin{equation*} \mathbf{X}_j^{(l)}= [\mathbf{h}_{x^j_1}^{(l)},\ldots,\mathbf{h}_{x^j_{|\mathcal{X}^j|}}^{(l)}],~ \mathbf{Y}_{i_k}^{(l)}= [\mathbf{h}_{y^{i_k}_1}^{(l)},\ldots,\mathbf{h}_{y^{i_k}_{|\mathcal{X}^{i_k}|}}^{(l)}]. \end{equation*}\] Every message \(m_{x^{^j}_t, y^{i_k}_s }\) corresponds to the entry \([G_k]_{st}\) of matrix \(G_k\). In other words, there is a one-to-one correspondence between non-zero entries of matrix \(G_k\) and messages \(m_{x^{^j}_t, y^{i_k}_s }\).
It follows from Section 5.2 that computing \(\{m_x^k\}_{k=1}^n\) corresponds to a merge node \(\mathcal{M}_{Id_j,G_k}\colon \mathcal{C}^j\times \mathcal{C}^{i_k}\to \mathcal{C}^j\) that performs the computations determined via \(\alpha_k\) and \(\bigoplus\), and yields \[\begin{equation*} \mathbf{m}_j^k=[m_{x^j_1}^k,\ldots,m_{x^j_{|\mathcal{X}^j|}}^k]= \mathcal{M}_{Id_j,G_k}(\mathbf{X}_j^{(l)},\mathbf{Y}_{i_k}^{(l)}) \in \mathcal{C}^{j}. \end{equation*}\] At this stage, we have \(n\) \(j\)-cochains \(\{\mathbf{m}_j^k\}_{k=1}^n\). Equations (6.3) and (6.4) merge these cochains with the input \(j\)-cochain \(\mathbf{X}_j^{(l)}\). Specifically, computing \(m_x\) in Equation (6.3) corresponds to \(n-1\) applications of merge nodes of the form \(\mathcal{M}_{Id_k,Id_k}\colon\mathcal{C}^j \times \mathcal{C}^j \to \mathcal{C}^j\) on the cochains \(\{\mathbf{m}_j^k\}_{k=1}^n\). Explicitly, we first merge \(\mathbf{m}_j^1\) and \(\mathbf{m}_j^2\) to obtain \(\mathbf{n}_j^1=\mathcal{M}_{Id_j,Id_j}(\mathbf{m}_j^1,\mathbf{m}_j^2)\). Next, we merge the \(j\)-cochain \(\mathbf{n}_j^1\) with the \(j\)-cochain \(\mathbf{m}_j^3\), and so on. The final merge node in this stage performs the merge \(\mathbf{n}_j^{n-1}=\mathcal{M}_{Id_j,Id_j}(\mathbf{n}_j^{n-2},\mathbf{m}_j^n)\), which is \(\mathbf{m}_j = [ m_{x_1^j},\ldots, m_{x_{|\mathcal{X}^j|}^j }]\)5. Finally, computing \(\mathbf{X}_j^{(l+1)}\) is realized by a merge node \(\mathcal{M}_{(Id_j,Id_j)}(\mathbf{m}_j, \mathbf{X}_j^{(l)})\) whose computations are determined by function \(\beta\) of Equation (6.4).
Theorem 6.1 shows that higher-order message-passing networks defined on CCs can be constructed from the elementary tensor operations, and hence they are special cases of CCNNs. We state this result formally in Theorem 6.2.
Theorem 6.2 (Higher-order message passing and CCNNs) A higher-order message-passing neural network is a CCNN.
It follows from Theorem 6.2 that higher-order message-passing neural networks defined on higher-order domains that are less general than CCs (such as simplicial complexes, cell complexes and hypergraphs) are also special cases of CCNNs. Thus, tensor diagrams, as introduced in Definition 5.2, form a general diagrammatic method for expressing neural networks defined on commonly studied higher-order domains.
Theorem 6.3 (Message-passing neural networks and tensor diagrams) Message-passing neural networks defined on simplicial complexes, cell complexes or hypergraphs can be expressed in terms of tensor diagrams and their computations can be realized in terms of the three elementary tensor operators.
Proof. The conclusion follows from Theorem 6.2 and from the fact that simplicial complexes, cell complexes and hypergraphs can be realized as special cases of CCs.
Theorems 6.2 and 6.3 put forward a unifying TDL framework based on tensor diagrams, thus providing scope for future developments. For instance, (Papillon et al. 2023) have already used our framework to express existing TDL architectures for simplicial complexes, cell complexes and hypergraphs in terms of tensor diagrams.
6.3 Merge nodes and higher-order message passing: a qualitative comparison
Higher-order message passing, as given in Definition 6.1, provides an update rule to obtain the vector \(\mathbf{h}_x^{l+1}\) from vector \(\mathbf{h}_x^{l}\) using a set of neighborhood vectors \(\mathbf{h}_y^{l}\) determined by \(\mathcal{N}(x)\). Clearly, this computational framework assumes that vectors \(\mathbf{h}_x^{(l)}\) and \(\mathbf{h}_{y}^{(l)}\) are provided as inputs. In other words, performing higher-order message passing according to Definition 6.1 requires the cochain \(\mathbf{X}_j^{(l)} \in \mathcal{C}^{j}\) in the target domain as well as the cochains \(\mathbf{Y}_{i_k}^{(l)} \in \mathcal{C}^{i_k}\) in order to compute the updated \(j\)-cochain \(\mathbf{X}_j^{(l+1)}\). On the other hand, performing a merge node computation requires a cochain vector \((\mathbf{H}_{i_1},\mathbf{H}_{i_2})\), as seen from Equation (5.1) and Definition 5.4.
The difference between these two computational frameworks might seem notational and the message passing perspective might seem more intuitive, especially when working with graph-based models. However, we argue that the merge node framework is more natural and flexible computationally in the presence of a custom higher-order network architecture. To illustrate this, we consider the example visualized in Figure 6.2.
In Figure 6.2, the displayed neural network has a cochain input vector \((\mathbf{H}_0,\mathbf{H}_2) \in \mathcal{C}^0 \times \mathcal{C}^2\). In the first layer, the neural network computes the cochain \(\mathbf{H}_1 \in \mathcal{C}^1\), while in the second layer it computes the cochain \(\mathbf{H}_3\in \mathcal{C}^3\). To obtain cochain \(\mathbf{H}_1\) in the first layer, we need to consider the neighborhood functions induced by \(B_{0,1}^T\) and \(B_{1,2}\). However, if we employ Equations (6.1) and (6.2) to perform the computations determined by the first layer of the tensor diagram in Figure 6.2, then we notice that no cochain is provided on \(\mathcal{C}^1\) as part of the input. Hence, when applying Equations (6.1) and (6.2), a special treatment is required since the vectors \(\mathbf{h}_{x^1_j}\) have not been computed yet. Note that such an artifact is not present in GNNs, since they often update node features, which are typically provided as part of the input. To be specific, in GNNs, the first two arguments in the update rule of Equation (6.1) are cochains that are supported on the 0-cells of the underlying graph.
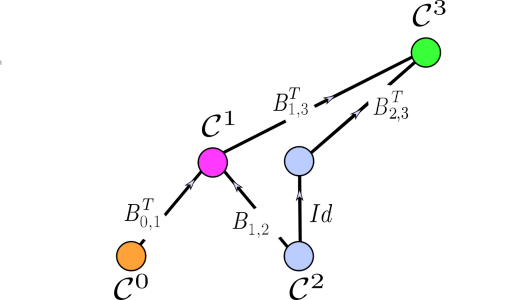
FIGURE 6.2: The depicted neural network can be realized as a composition of two merge nodes. More specifically, the input is a cochain vector \((\mathbf{H}_0,\mathbf{H}_2)\). The first merge node computes the 1-chain \(\mathbf{H}_1 = \mathcal{M}_{B_{0,1}^T,B_{1,2}} (\mathbf{H}_0,\mathbf{H}_2)\). Similarly, the second merge node \(\mathcal{M}_{B_{1,3}^T, B_{2,3}} \colon\mathcal{C}^1 \times \mathcal{C}^2 \to \mathcal{C}^3\) computes the 3-cochain \(\mathbf{H}_3=\mathcal{M}_{B_{1,3}^T, B_{2,3}}(\mathbf{H}_1,\mathbf{H}_2)\). The merge node perspective allows to compute a cochain supported on the 1-cells and 3-cells without having initial cochains of these cells. On the other hand, the higher-order message-passing framework has two major constraints: it assumes as input initial cochains supported on all cells of all dimensions of the domain, and it updates all cochains supported on all cells of all dimensions of the input domain at every iteration.
Similarly, to compute the cochain \(\mathbf{H}_3 \in \mathcal{C}^3\) in the second layer of Figure 6.2, we must consider the neighborhood functions induced by \(B_{1,3}^T\) and \(B_{2,3}\), and we must use the cochain vector \((\mathbf{H}_1,\mathbf{H}_2)\). This means that the cochains \(\mathbf{H}_1\) and \(\mathbf{H}_3\) resulting from the computation of the neural network given in Figure 6.2 are not obtained from an iterative process. Further, the input vectors \(\mathbf{H}_0\) and \(\mathbf{H}_2\) are never updated at any step of the procedure. Finally, the cochains \(\mathbf{H}_1\) and \(\mathbf{H}_3\) are never updated. From the perspective of update rules such as the ones appearing in the higher-order message passing framework (Definition 6.1), this setting is unnatural in the sense that it assumes initial cochains supported on all cells of all dimensions as input, and in the sense that it updates all cochains supported on all cells in the complex of the input domain at every iteration.
In practice, such difficulties in using the higher-order message passing framework can be overcome with ad hoc engineering solutions based on turning on and off iterations on certain cochains or based on introducing auxiliary cochains. The merge node is designed to overcome these limitations. Specifically, from the merge node perspective, we can think of the first layer of Figure 6.2 as a function \(\mathcal{M}_{B_{0,1}^T,B_{1,2}}\colon \mathcal{C}^0 \times \mathcal{C}^1 \to \mathcal{C}^1\); see Equation (5.2). The function \(\mathcal{M}_{B_{0,1}^T,B_{1,2}}\) takes as input the cochain vector \((\mathbf{H}_0,\mathbf{H}_2)\), and computes the 1-chain \(\mathbf{H}_1 = \mathcal{M}_{B_{0,1}^T,B_{1,2}} (\mathbf{H}_0,\mathbf{H}_2)\). Similarly, we compute the 3-cochain \(\mathbf{H}_3=\mathcal{M}_{B_{1,3}^T, B_{2,3}}(\mathbf{H}_1,\mathbf{H}_2)\) using a merge node \(\mathcal{M}_{B_{1,3}^T, B_{2,3}} \colon \mathcal{C}^1 \times \mathcal{C}^2 \to \mathcal{C}^3\).
6.4 Attention higher-order message passing and CCANNs
Here, we demonstrate the connection between higher-order message passing (Definition 6.1) and CCANNs (Section 5.5). Initially, we introduce an attention version of Definition 6.1.
Definition 6.3 (Attention higher-order message passing on a CC) Let \(\mathcal{X}\) be a CC. Let \(\mathcal{N}=\{ \mathcal{N}_1,\ldots,\mathcal{N}_n\}\) be a set of neighborhood functions defined on \(\mathcal{X}\). Let \(x\) be a cell and \(y\in \mathcal{N}_k(x)\) for some \(\mathcal{N}_k \in \mathcal{N}\). A message \(m_{x,y}\) between cells \(x\) and \(y\) is a computation that depends on these two cells or on the data supported on them. Denote by \(\mathcal{N}(x)\) the multi-set \(\{\!\!\{ \mathcal{N}_1(x) , \ldots , \mathcal{N}_n (x) \}\!\!\}\), and by \(\mathbf{h}_x^{(l)}\) some data supported on the cell \(x\) at layer \(l\). Attention higher-order message passing on \(\mathcal{X}\), induced by \(\mathcal{N}\), is defined via the following four update rules: \[\begin{align} m_{x,y} &= \alpha_{\mathcal{N}_k}(\mathbf{h}_x^{(l)},\mathbf{h}_y^{(l)}), \tag{6.5} \\ m_{x}^k &= \bigoplus_{y \in \mathcal{N}_k(x)} a^k(x,y) m_{x,y}, \; 1\leq k \leq n , \tag{6.6} \\ m_{x} &= \bigotimes_{ \mathcal{N}_k \in \mathcal{N} } b^k m_x^k , \tag{6.7} \\ \mathbf{h}_x^{(l+1)} &= \beta (\mathbf{h}_x^{(l)}, m_x) . \tag{6.8} \end{align}\] Here, \(a^k \colon \{x\} \times \mathcal{N}_k(x)\to [0,1]\) is a higher-order attention function (Definition 5.9), \(b^k\) are trainable attention weights satisfying \(\sum_{k=1}^n b^k=1\), \(\bigoplus\) is a permutation-invariant aggregation function, \(\bigotimes\) is an aggregation function, \(\alpha_{\mathcal{N}_k}\) and \(\beta\) are differentiable functions.
Definition 6.3 distinguishes two types of attention weights. The first type is determined by the function \(a^k\). The attention weight \(a^k(x,y)\) of Equation (6.6) depends on the neighborhood function \(\mathcal{N}_k\) and on cells \(x\) and \(y\). Further, \(a^k(x,y)\) determines the attention a cell \(x\) pays to its surrounding neighbors \(y\in\mathcal{N}_k\), as determined by the neighborhood function \(\mathcal{N}_k\). The CC-attention push-forward operations defined in Section 5.5 are a particular parameterized realization of these weights. On the other hand, the weights \(b^k\) of Equation (6.7) are only a function of the neighborhood \(\mathcal{N}_k\), and therefore determine the attention that cell \(x\) pays to the information obtained from each neighborhood function \(\mathcal{N}_k\). In our CC-attention push-forward operations given in Section 5.5, we set \(b^k\) equal to one. However, the notion of merge node (Definition 5.4) can be easily extended to introduce a corresponding notion of attention merge node, which in turn can be used to realize Equation (6.7) in practice. Note that the attention determined by weights \(b^k\) is unique to higher-order domains, and does not arise in graph-based attention models.