B Lifting maps

Lifting refers to the process of mapping a featured domain to another featured domain via a well-defined procedure. This section shows how we can lift a given domain to a CC or cell complex. Such lifting is useful as it allows CCNNs to be applied to common topological domains, including graphs and cell/simplicial complexes. This section only scratches the surface, as there remain many lifting constructions to be explored. We refer the reader to (Ferri, Bergomi, and Zu 2018) for examples of lifting graphs to simplicial complexes.

B.1 n-hop CC of a graph

Let $\mathcal{G}=(V(\mathcal{G}),E(\mathcal{G}))$ be a graph and $n\geq 2$ an integer. The $n$-hop CC of $\mathcal{G}$, denoted by $\mbox{CC}_{n-\mbox{hop}}(\mathcal{G})$, is the CC whose $0$-cells, $1$-cells, and $n$-cells are the nodes of $\mathcal{G}$, edges of $\mathcal{G}$, and set nodes in $n$-hop neighborhoods of the nodes in $\mathcal{G}$, respectively. It is easy to verify that $\mbox{CC}_{n-\mbox{hop}}(\mathcal{G})$ is a CC of dimension $n$. Figure B.1(a) visualizes the $1$-hop CC of a graph.

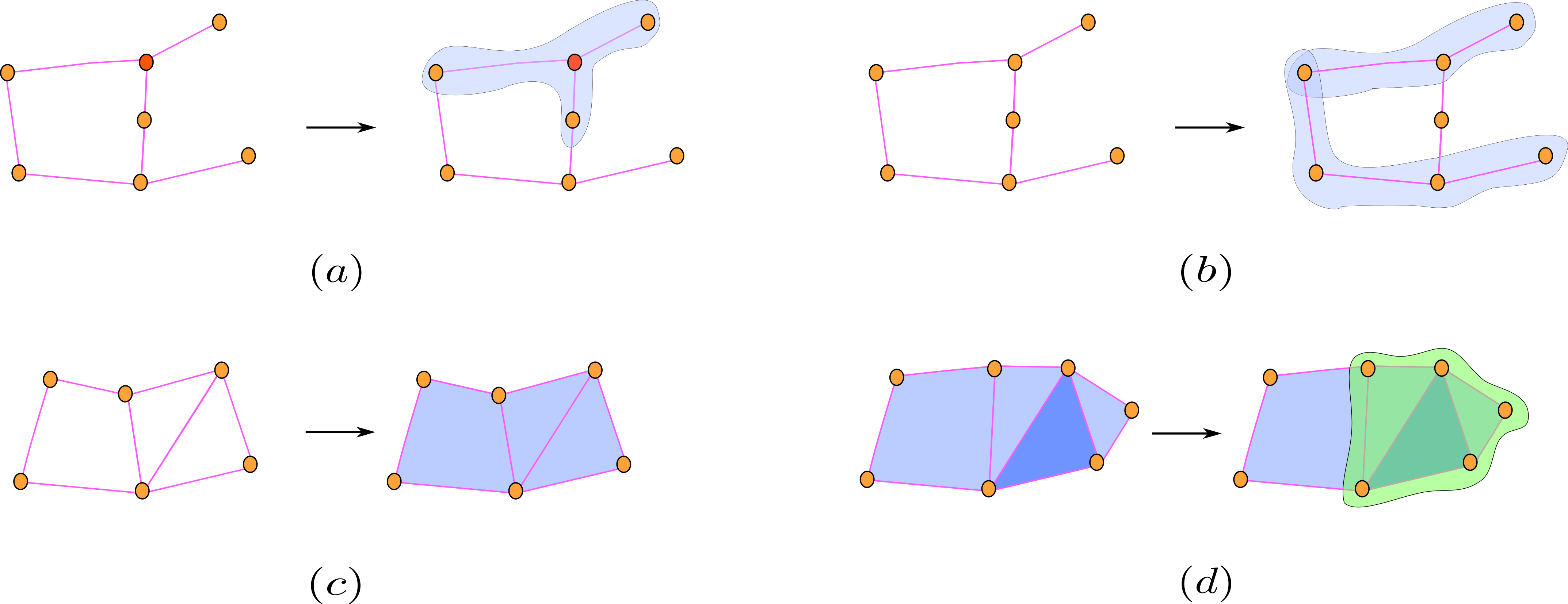
FIGURE B.1: Examples of lifting domains to CCs and cell complexes. (a): The $1$-hop neighborhood of the red node can be considered as a 2-cell that we can augment to the graph. Adding such 2-cells to a graph yields a CC called the 1-hop neighborhood of the graph. (b): A path on a graph of length more than two can be considered as a 2-cell that we can augment to the graph. Adding such 2-cells to a graph yields a CC called a path-based CC of the graph. (c): A loop in a graph (i.e., a closed path with no repeating edges) can be considered as a 2-cell that we can augment to the graph. Adding such 2-cells to a graph yields a CC called a loop-based CC of the graph. (d): For every blue 2-cell of a simplicial complex, we introduce a green 3-cell obtained by considering the 1-coface of the 2-cell. Adding such 3-cells to a simplicial complex yields a CC of dimension three called the coface CC of the simplicial complex.

B.2 Path-based and subgraph-based CC of a graph

Let $\mathcal{G}=(V(\mathcal{G}),E(\mathcal{G}))$ be a graph. A natural CC structure on $\mathcal{G}$ considers paths of $\mathcal{G}$. We define a path-based CC of $\mathcal{G}$, denoted by $\mbox{CC}_p(\mathcal{G})$, to be a CC consisting of $0$-cells, $1$-cells and $2$-cells specified as follows. First, $\mathcal{X}^0$ and $\mathcal{X}^1$ in $\mbox{CC}_p(\mathcal{G})$ are the sets of nodes and edges of $\mathcal{G}$, respectively. We now explain how to construct a $2$-cell in $\mbox{CC}_p(\mathcal{G})$. Let $P$ be a path in $\mathcal{G}$ with length larger than or equal to two (i.e., with two or more edges). An element $x_P$ in $\mathcal{X}^2$ induced by $P$ is defined to be $x_P=\cup_{v\in P }\{v\}$. The set $\mathcal{X}^2$ in $\mbox{CC}_p(\mathcal{G})$ is a non-empty collection of elements $x_P$. It is easy to verify that $\mbox{CC}_p(\mathcal{G})$ is a CC with $\dim(\mbox{CC}_p(\mathcal{G}))=2$. Note that we may replace the path $P$ by a tree/subgraph of graph $\mathcal{G}$ and obtain a similar CC structure induced by the tree/subgraph of $\mathcal{G}$. Figure B.1(b) shows an example of a path-based CC of a graph.

B.3 Loop-based CC of a graph

Let $\mathcal{G}=(V(\mathcal{G}),E(\mathcal{G}))$ be a graph. We associate a CC structure with $\mathcal{G}$ that considers loops in $\mathcal{G}$. We define a loop-based CC of $\mathcal{G}$, denoted by $\mbox{CC}_{loop}(\mathcal{G})$, to be a CC consisting of $0$-cells, $1$-cells and $2$-cells specified as follows. First, we set $\mathcal{X}^0$ and $\mathcal{X}^1$ in $\mbox{CC}_{loop}(\mathcal{G})$ to be the nodes and edges of $\mathcal{G}$, respectively. We now explain how to construct a $2$-cell in $\mbox{CC}_{loop}(\mathcal{G})$. A 2-cell in $\mbox{CC}_{loop}(\mathcal{G})$ is a set $C=\{x^0_1, \ldots , x^0_k\} \subset \mathcal{X}^0$ such that $\{x^0_i,x^0_{i+1}\}$, $1 \leq i \leq k - 1$, and $\{x^0_k, x^0_1\}$ are the only edges in $\mathcal{X}^1 \cap C$. The set $\mathcal{X}^2$ in $\mbox{CC}_{loop}(\mathcal{G})$ is a nonempty collection of elements $C$. It is easy to verify that $\mbox{CC}_{loop}(\mathcal{G})$ is a CC with $\dim(\mbox{CC}_{loop}(\mathcal{G}))=2$. Note that the sequence $(x^0_1, \ldots , x^0_k)$ defines a loop in $\mathcal{G}$. This loop is called the loop that characterizes the 2-cell $C=\{x^0_1, \ldots , x^0_k\}$. Similar constructions are suggested in (Aschbacher 1996; Basak 2010; Savoy 2021; T. Mitchell Roddenberry, Schaub, and Hajij 2022). In fact, it is easy to confirm that every 2-dimensional regular cell complex can be constructed in this manner (T. Mitchell Roddenberry, Schaub, and Hajij 2022). Figure B.1(c) shows an example of a loop-based CC of a graph.

B.4 Coface CC of a simplicial complex or of a CC

Here, we describe a method to lift a simplicial complex of dimension two to a CC of dimension three. This method can be easily generalized to other dimensions. For a simplicial complex $\mathcal{Y}$ of dimension two, the coface CC of $\mathcal{Y}$, denoted by $\mbox{CC}_{SC}( \mathcal{Y})$, is defined as follows. $\mathcal{Y}^0$, $\mathcal{Y}^1$, and $\mathcal{Y}^2$ in $\mbox{CC}_{SC}( \mathcal{Y})$ are the nodes, the edges, and the triangles in $\mathcal{Y}$, respectively. We now explain how to construct a $3$-cell in $\mbox{CC}_{SC}( \mathcal{Y})$. Let $x^2$ be a 2-cell in $\mathcal{Y}$. The 3-cell in $\mbox{CC}_{SC}( \mathcal{Y})$ associated with $x^2$ is the union of all 0-cells in $\mathcal{N}_{co,1}(x^2) \cup x^2$. The set $\mathcal{Y}^3$ in $\mbox{CC}_{SC}( \mathcal{Y})$ is defined as the set of all 3-cells associated with all 2-cells $x^2$ in $\mathcal{Y}$. It is easy to verify that $\mbox{CC}_{SC}(\mathcal{Y})$ is a CC with $\dim(\mbox{CC}_{SC}(\mathcal{Y}) )=3$. A similar lifting construction can be defined to augment any CC of dimension $n$ with $(n+1)$-cells in order to obtain a CC of dimension $n+1$.

B.5 Augmentation of CCs by higher-rank cells

The lifting methods proposed in Sections B.2, B.3, and B.4 can be described abstractly under a single general lifting construction. Specifically, the essence of all these lifting methods is to augment the underlying CC $\mathcal{X}$ with new cells that have a rank of $\dim(\mathcal{X})+1$. Proposition B.1 formalizes the general lifting construction.

Proposition B.1 (Augmenting a CC) Let $S$ be a nonempty set and $(S,\mathcal{X},\mbox{rk})$ a CC of dimension $n$ defined on $S$. Consider a set $\mathcal{X}^{n+1} \subset \mathcal{P}(S)$ such that if $x\in\mathcal{X}$ and $y \in \mathcal{X}^{n+1}$ with $x\subseteq y$, then $x\subsetneq y$. Further, consider a map $\hat{\mbox{rk}}\colon \mathcal{X}\cup \mathcal{X}^{n+1}\to \mathbb{Z}_{\ge 0}$ that satisfies $\hat{\mbox{rk}}(x)= \mbox{rk}(x)$ for all $x\in\mathcal{X}$ and $\hat{\mbox{rk}}(x)=n+1$ for all $x \in \mathcal{X}^{n+1}$. For $\mathcal{X}^{n+1}$ and $\hat{\mbox{rk}}$ satisfying such conditions, $(S,\mathcal{X}\cup \mathcal{X}^{n+1},\hat{\mbox{rk}} )$ is a CC of dimension $n+1$.

Proof. The proof follows directly from Definition 4.1.

Given a CC $\mathcal{X}$, we call a CC of the form $(S,\mathcal{X}\cup \mathcal{X}^{n+1},\hat{\mbox{rk}} )$, as constructed in Proposition B.1, a highest-rank augmented CC of $\mathcal{X}$. Note that Proposition B.1 provides a constructive and iterative method to build a CC of arbitrary dimension from a nonempty set $S$ of abstract points.

References

Aschbacher, Michael. 1996. “Combinatorial Cell Complexes.” In Progress in Algebraic Combinatorics, 1–80. Mathematical Society of Japan.

Basak, Tathagata. 2010. “Combinatorial Cell Complexes and Poincaré Duality.” Geometriae Dedicata 147 (1): 357–87.

Ferri, Massimo, Dott Mattia G. Bergomi, and Lorenzo Zu. 2018. “Simplicial Complexes from Graphs Towards Graph Persistence.” arXiv Preprint arXiv:1805.10716.

Roddenberry, T. Mitchell, Michael T. Schaub, and Mustafa Hajij. 2022. “Signal Processing on Cell Complexes.” In IEEE International Conference on Acoustics, Speech and Signal Processing.

Savoy, Maxime. 2021. “Combinatorial Cell Complexes: Duality, Reconstruction and Causal Cobordisms.” PhD thesis, École Polytechnique Fédérale de Lausanne.