Chapter 1 Introduction

In recent years, there has been an exponential growth in the amount of data available for computational analysis, including scientific data as well as common data types such as text, images, and audio. This abundance of data has empowered various fields, including physics, chemistry, computational social sciences, and biology, to make significant progress using machine learning techniques, primarily deep neural networks. As deep neural networks can effectively summarize and extract patterns from large data sets, they are suitable for many complex tasks. Initially, deep neural networks have been developed to learn from data supported on regular (Euclidean) domains, such as grids in images, sequences of text and time-series. These models, including convolutional neural networks (CNNs) (LeCun et al. 1998; Krizhevsky, Sutskever, and Hinton 2012; Simonyan and Zisserman 2014), recurrent neural networks (RNNs) (Bahdanau, Cho, and Bengio 2014; Sutskever, Vinyals, and Le 2014) and transformers (Vaswani et al. 2017), have proven highly effective in processing such Euclidean data (Goodfellow et al. 2016), resulting in unprecedented performance in various applications, most recently in chat-bots (e.g., ChatGPT (Adesso 2023)) and text-controlled image synthesis (Rombach et al. 2022).

However, scientific data in various fields are often structured differently and are not supported on regular Euclidean domains. As a result, adapting deep neural networks to process this type of data has been a challenge. Against this backdrop, geometric deep learning (GDL) (Zonghan Wu et al. 2020; Zhou et al. 2020; Bronstein et al. 2021) has emerged as an extension of deep learning models to non-Euclidean domains. To achieve this, GDL restricts the performed computations via principles of geometric regularity, such as symmetries, invariances, and equivariances. The GDL perspective allows for appropriate inductive biases to be imposed when working with arbitrary data domains, including sets (Qi et al. 2017; Rempe et al. 2020; H. Deng, Birdal, and Ilic 2018; Y. Zhao et al. 2022; Jiahui Huang et al. 2022), grids (Boscaini et al. 2015, 2016; Masci et al. 2015; Kokkinos et al. 2012; Shuman, Ricaud, and Vandergheynst 2016; Zhirong Wu et al. 2015; Monti et al. 2017), manifolds (Boscaini et al. 2015, 2016; Masci et al. 2015; Kokkinos et al. 2012; Shuman, Ricaud, and Vandergheynst 2016; Zhirong Wu et al. 2015; Monti et al. 2017), and graphs (Scarselli et al. 2008; Gallicchio and Micheli 2010; Zhou et al. 2020; Zonghan Wu et al. 2020; Boscaini et al. 2016; Monti et al. 2017; Bronstein et al. 2017; Kipf and Welling 2016). Graphs, in particular, have garnered interest due to their applicability in numerous scientific studies and their ability to generalize conventional grids. Accordingly, the development of graph neural networks (GNNs) (Bronstein et al. 2017; Kipf and Welling 2016) has remarkably enhanced our ability to model and analyze several types of data in which graphs naturally appear.

Despite the success of GDL and GNNs, seeing graphs through a purely geometric viewpoint yields a solely local abstraction and falls short of capturing non-local properties and dependencies in data. Topological data, including interactions of edges (in graphs), triangles (in meshes) or cliques, arise naturally in an array of novel applications in complex physical systems (Battiston et al. 2021; Lambiotte, Rosvall, and Scholtes 2019), traffic forecasting (W. Jiang and Luo 2022), social influence (Zhu et al. 2018), protein interaction (Murgas, Saucan, and Sandhu 2022), molecular design (Schiff et al. 2020), visual enhancement (Efthymiou et al. 2021), recommendation systems (La Gatta et al. 2022), and epidemiology (S. Deng et al. 2020). To natively and effectively model such data, we are bound to go beyond graphs and consider qualitative spatial properties remaining unchanged under some geometric transformations. In other words, we need to consider the topology of data (G. Carlsson 2009) to formulate neural network architectures capable of extracting semantic meaning from complex data.

One approach to extract more global information from data is to go beyond graph-based abstractions and consider extensions of graphs, such as simplicial complexes, cell complexes, and hypergraphs, generalizing most data domains encountered in scientific computations (Bick et al. 2021; Battiston et al. 2020; Benson, Gleich, and Higham 2021; Torres et al. 2021). The development of machine learning models to learn from data supported on these topological domains (Feng et al. 2019; Bunch et al. 2020; T. Mitchell Roddenberry, Schaub, and Hajij 2022; Schaub et al. 2020, 2021; Billings et al. 2019; Hacker 2020; Hajij, Istvan, and Zamzmi 2020; Ebli, Defferrard, and Spreemann 2020; T. Mitchell Roddenberry, Glaze, and Segarra 2021; L. Giusti, Battiloro, Testa, et al. 2022; Yang and Isufi 2023) is a rapidly growing new frontier, to which we refer hereafter as topological deep learning (TDL). TDL intertwines several research areas, including topological data analysis (TDA) (Edelsbrunner and Harer 2010; G. Carlsson 2009; Dey and Wang 2022a; Love et al. 2023a; Ghrist 2014), topological signal processing (Schaub and Segarra 2018; Yang et al. 2021; Schaub et al. 2022; T. Mitchell Roddenberry, Schaub, and Hajij 2022; Barbarossa and Sardellitti 2020a; Robinson 2014; Sardellitti and Barbarossa 2022), network science [Skardal et al. (2021); Lambiotte, Rosvall, and Scholtes (2019); Barabási (2013); Battiston et al. (2020); Bick et al. (2021); Bianconi (2021); Benson, Gleich, and Leskovec (2016); De Domenico et al. (2016); Bao et al. (2022); Oballe et al. (2021)}, and geometric deep learning (S.-X. Zhang et al. 2020; Cao et al. 2020; Fey and Lenssen 2019; Loukas 2019; P. W. Battaglia et al. 2018; Morris et al. 2019; P. Battaglia et al. 2016).

Despite the growing interest in TDL, a broader synthesis of the foundational principles of these ideas has not been established so far. We argue that this is a deficiency that inhibits progress in TDL, as it makes it challenging to draw connections between different concepts, impedes comparisons, and makes it difficult for researchers of other fields to find an entry point to TDL. Hence, in this paper, we aim to provide a foundational overview over the principles of TDL, serving not only as a unifying framework for the many exciting ideas that have emerged in the literature over recent years, but also as a conceptual starting point to promote the exploration of new ideas. Ultimately, we hope that this work will contribute to the accelerated growth in TDL, which we believe would be a key enabler of transferring deep learning successes to an enlarged range of application scenarios.

By drawing inspiration from traditional topological notions in algebraic topology (Ghrist 2014; Hatcher 2005) and recent advancements in higher-order networks (Battiston et al. 2020, 2021; Torres et al. 2021; Bick et al. 2021), we first introduce combinatorial complexes (CCs) as the major building blocks of our TDL framework. CCs constitute a novel topological domain that unifies graphs, simplicial and cell complexes, and hypergraphs as special cases, as illustrated in Figure 1.11. Similar to hypergraphs, CCs can encode arbitrary set-like relations between collections of abstract entities. Moreover, CCs permit the construction of hierarchical higher-order relations, analogous to those found in simplicial and cell complexes. Hence, CCs generalize and combine the desirable traits of hypergraphs and cell complexes.

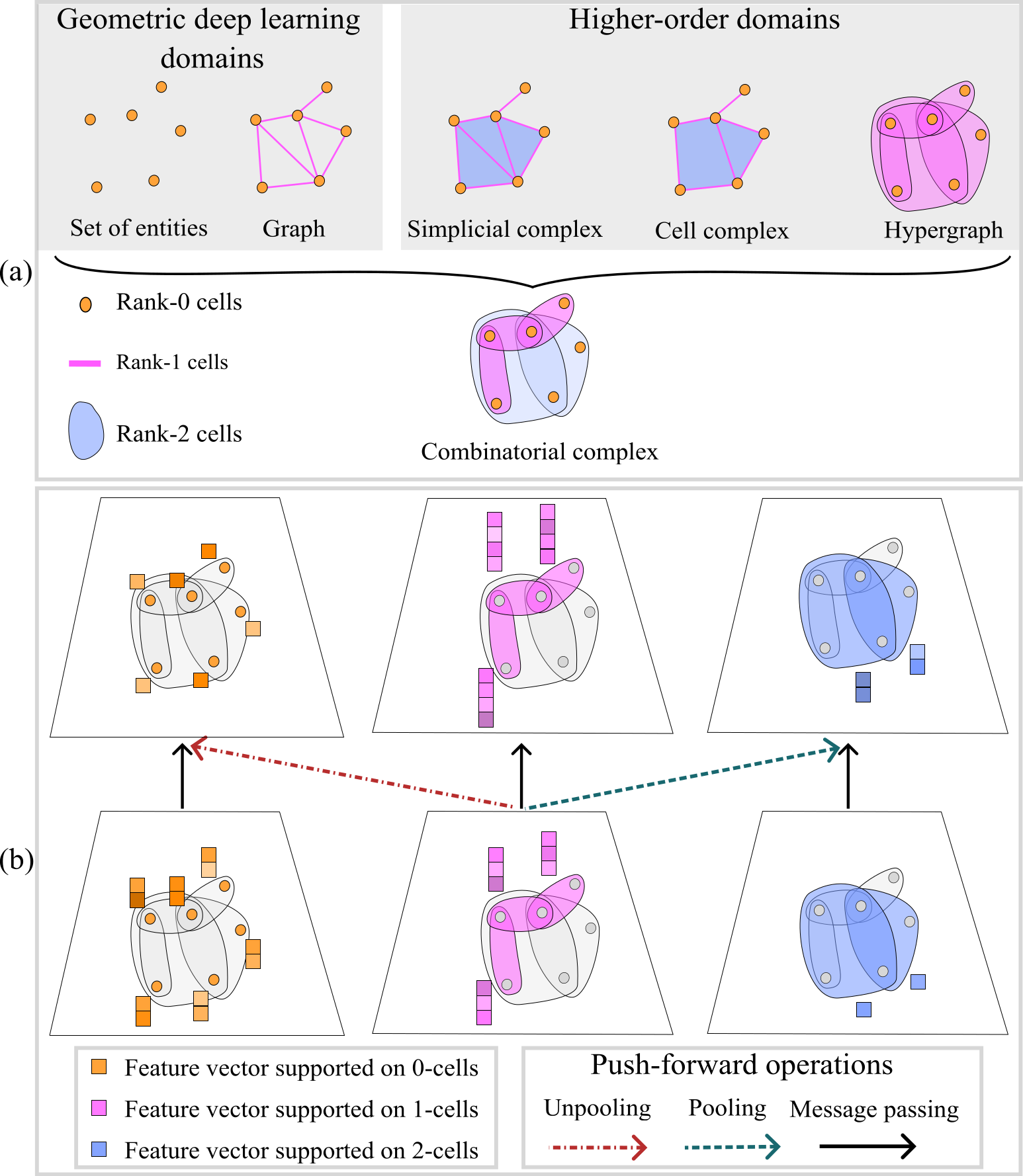
A graphical abstract that visualizes our main contributions. (a): Different mathematical structures can be used to represent relations between abstract entities. Sets have entities with no connections, graphs encode binary relations between vertices, simplicial and cell complexes model hierarchical higher-order relations, and hypergraphs accommodate arbitrary set-type relations with no hierarchy. We introduce combinatorial complexes (CCs), which generalize graphs, simplicial and cell complexes, and hypergraphs. CCs are equipped with set-type relations as well as with a hierarchy of these relations. (b): By utilizing the hierarchical and topological structure of CCs, we introduce the push-forward operation, a fundamental building block for higher-order message-passing protocols and for (un)pooling operations on CCs. Our push-forward operations on CCs enable us to construct combinatorial complex neural networks (CCNNs), which provide a general conceptual framework for topological deep learning on higher-order domains.

FIGURE 1.1: A graphical abstract that visualizes our main contributions. (a): Different mathematical structures can be used to represent relations between abstract entities. Sets have entities with no connections, graphs encode binary relations between vertices, simplicial and cell complexes model hierarchical higher-order relations, and hypergraphs accommodate arbitrary set-type relations with no hierarchy. We introduce combinatorial complexes (CCs), which generalize graphs, simplicial and cell complexes, and hypergraphs. CCs are equipped with set-type relations as well as with a hierarchy of these relations. (b): By utilizing the hierarchical and topological structure of CCs, we introduce the push-forward operation, a fundamental building block for higher-order message-passing protocols and for (un)pooling operations on CCs. Our push-forward operations on CCs enable us to construct combinatorial complex neural networks (CCNNs), which provide a general conceptual framework for topological deep learning on higher-order domains.

In addition, we introduce the necessary operators to construct deep neural networks for learning features and abstract summaries of input anchored on CCs. Such operators provide convolutions, attention mechanisms, message-passing schemes as well as the means for incorporating invariances, equivariances, or other geometric regularities. Specifically, our novel push-forward operation allows pushing data across different dimensions, thus forming an elementary building block upon which higher-order message-passing protocols and (un)pooling operations are defined on CCs. The resulting learning machines, which we call combinatorial complex neural networks (CCNNs), are capable of learning abstract higher-order data structures, as clearly demonstrated in our experimental evaluation.

We envisage our contributions to be a platform encouraging researchers and practitioners to extend our CCNNs, and invite the community to build upon our work to expand TDL on higher-order domains. Our contributions, which are also visually summarized in Figure 1.1, are the following:

  • First, we introduce CCs as domains for TDL. We characterize CCs and their properties, and explain how they generalize major existing domains, such as graphs, hypergraphs, simplicial and cell complexes. CCs can thus serve as a unifying starting point that enables the learning of expressive representations of topological data.
  • Second, using CCs as domains, we construct CCNNs, an abstract class of higher-order message-passing neural networks that provide a unifying blueprint for TDL models based on hypergraphs and cell complexes.
    • Based upon a push-forward operator defined on CCs, we introduce convolution, attention, pooling and unpooling operators for CCNNs.
    • We formalize and investigate permutation and orientation equivariance of CCNNs, paving the way to future work on geometrization of CCNNs.
    • We show how CCNNs can be intuitively constructed via graphical notation.
  • Third, we evaluate our ideas in practical scenarios.
    • We release the source code of our framework as three supporting Python libraries: TopoNetX, TopoEmbedX and TopoModelX.
    • We show that CCNNs attain competing predictive performance against state-of-the-art task-specific neural networks in various applications, including shape analysis and graph learning.
    • We establish connections between our work and classical constructions in TDA, such as the mapper (Singh et al. 2007). Particularly, we realize the mapper construction in terms of our TDL framework and demonstrate how it can be utilized in higher-order (un)pooling on CCs.
    • We demonstrate the reducibility of any CC to a special graph called the Hasse graph. This enables the characterization of certain aspects of CCNNs in terms of graph-based models, allowing us to reduce higher-order representation learning to graph representation learning (using an enlarged computational graph).

Glossary. Prior to delving into more details, we present the elementary terminologies of already established concepts used throughout the paper. Some of these terms are revisited formally in Chapter 3. Appendix A provides notation and terminology glossaries for novel ideas put forward by the paper.

Cell complex: a topological space obtained as a disjoint union of topological disks (cells), with each of these cells being homeomorphic to the interior of a Euclidean ball. These cells are attached together via attaching maps in a locally reasonable manner.

Domain: the underlying space where data is typically supported.

Entity or vertex: an abstract point; it can be thought as an element of a set.

Graph or network: a set of entities (vertices) together with a set of edges representing binary relations between the vertices.

Hierarchical structure on a topological domain: an integer-valued function that assigns a positive integer (rank) to every relation in the domain such that higher-order relations are assigned higher rank values. For instance, a simplicial complex admits a hierarchical structure induced by the cardinality of its simplices.

Higher-order network/topological domain: generalization of a graph that captures (binary and) higher-order relations between entities. Simplicial/cell complexes and hypergraphs are examples of higher-order networks.

Hypergraph: a set of entities (vertices) and a set of hyperedges representing binary or higher-order relations between the vertices.

Message passing: a computational framework that involves passing data, `messages’, among neighbor entities in a domain to update the representation of each entity based on the messages received from its neighbors.

Relation or cell: a subset of a set of entities (vertices). A relation is called binary if its cardinality is equal to two. A relation is called higher-order if its cardinality is greater than two.

Set-type relation: a higher-order network is said to have set-type relations if the existence of a relation is not implied by another relation in the network; e.g., hypergraphs admit set-type relations.

Simplex: a generalization of a triangle or tetrahedron to arbitrary dimensions; e.g., a simplex of dimension zero, one, two, or three is a point, line segment, triangle, or tetrahedron, respectively.

Simplicial complex: a collection of simplices such that every face of each simplex in the collection is also in the collection, and the intersection of any two simplices in the collection is either empty or a face of both simplices.

Topological data: feature vectors supported on relations in a topological domain.

Topological deep learning: the study of topological domains using deep learning techniques, and the use of topological domains to represent data in deep learning models.

Topological neural network: a deep learning model that processes data supported on a topological domain.

References

Adesso, Gerardo. 2023. “Towards the Ultimate Brain: Exploring Scientific Discovery with ChatGPT AI.” AI Magazine 44 (3): 328–42. https://onlinelibrary.wiley.com/doi/abs/10.1002/aaai.12113.
Bahdanau, Dzmitry, Kyunghyun Cho, and Yoshua Bengio. 2014. “Neural Machine Translation by Jointly Learning to Align and Translate.” arXiv Preprint arXiv:1409.0473. https://arxiv.org/abs/1409.0473.
Bao, Xiaoge, Qitong Hu, Peng Ji, Wei Lin, Jürgen Kurths, and Jan Nagler. 2022. “Impact of Basic Network Motifs on the Collective Response to Perturbations.” Nature Communications 13 (1): 5301.
Barabási, Albert-László. 2013. “Network Science.” Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 371 (1987): 20120375.
Barbarossa, Sergio, and Stefania Sardellitti. 2020a. “Topological Signal Processing over Simplicial Complexes.” IEEE Transactions on Signal Processing 68: 2992–3007.
Battaglia, Peter W., Jessica B. Hamrick, Victor Bapst, Alvaro Sanchez-Gonzalez, Vinicius Zambaldi, Mateusz Malinowski, Andrea Tacchetti, et al. 2018. “Relational Inductive Biases, Deep Learning, and Graph Networks.” arXiv Preprint arXiv:1806.01261.
Battaglia, Peter, Razvan Pascanu, Matthew Lai, Danilo Jimenez Rezende, and Koray kavukcuoglu. 2016. “Interaction Networks for Learning about Objects, Relations and Physics.” In Proceedings of the 30th International Conference on Neural Information Processing Systems, 4509–17. NIPS’16. Red Hook, NY, USA: Curran Associates Inc.
Battiston, Federico, Enrico Amico, Alain Barrat, Ginestra Bianconi, Guilherme Ferraz de Arruda, Benedetta Franceschiello, Iacopo Iacopini, et al. 2021. “The Physics of Higher-Order Interactions in Complex Systems.” Nature Physics 17 (10): 1093–98.
Battiston, Federico, Giulia Cencetti, Iacopo Iacopini, Vito Latora, Maxime Lucas, Alice Patania, Jean-Gabriel Young, and Giovanni Petri. 2020. “Networks Beyond Pairwise Interactions: Structure and Dynamics.” Physics Reports 874: 1–92.
Benson, Austin R., David F. Gleich, and Desmond J. Higham. 2021. “Higher-Order Network Analysis Takes Off, Fueled by Classical Ideas and New Data.” arXiv Preprint arXiv:2103.05031.
Benson, Austin R., David F. Gleich, and Jure Leskovec. 2016. “Higher-Order Organization of Complex Networks.” Science 353 (6295): 163–66.
Bianconi, Ginestra. 2021. Higher-Order Networks. Cambridge University Press.
Bick, Christian, Elizabeth Gross, Heather A Harrington, and Michael T Schaub. 2021. “What Are Higher-Order Networks?” arXiv Preprint arXiv:2104.11329.
Billings, Jacob Charles Wright, Mirko Hu, Giulia Lerda, Alexey N. Medvedev, Francesco Mottes, Adrian Onicas, Andrea Santoro, and Giovanni Petri. 2019. “Simplex2Vec Embeddings for Community Detection in Simplicial Complexes.” arXiv Preprint arXiv:1906.09068.
Boscaini, Davide, Jonathan Masci, Simone Melzi, Michael M Bronstein, Umberto Castellani, and Pierre Vandergheynst. 2015. “Learning Class-Specific Descriptors for Deformable Shapes Using Localized Spectral Convolutional Networks.” Computer Graphics Forum 34 (5): 13–23.
Boscaini, Davide, Jonathan Masci, Emanuele Rodolà, and Michael Bronstein. 2016. “Learning Shape Correspondence with Anisotropic Convolutional Neural Networks.” In Advances in Neural Information Processing Systems, 3189–97.
Bronstein, Michael M., Joan Bruna, Taco Cohen, and Petar Veličković. 2021. “Geometric Deep Learning: Grids, Groups, Graphs, Geodesics, and Gauges.” arXiv Preprint arXiv:2104.13478.
Bronstein, Michael M., Joan Bruna, Yann LeCun, Arthur Szlam, and Pierre Vandergheynst. 2017. “Geometric Deep Learning: Going Beyond Euclidean Data.” IEEE Signal Processing Magazine 34 (4): 18–42.
Bunch, Eric, Qian You, Glenn Fung, and Vikas Singh. 2020. “Simplicial 2-Complex Convolutional Neural Nets.” NeurIPS Workshop on Topological Data Analysis and Beyond.
Cao, Wenming, Zhiyue Yan, Zhiquan He, and Zhihai He. 2020. “A Comprehensive Survey on Geometric Deep Learning.” IEEE Access 8: 35929–49.
Carlsson, Gunnar. 2009. “Topology and Data.” Bulletin of the American Mathematical Society 46 (2): 255–308.
De Domenico, Manlio, Clara Granell, Mason A Porter, and Alex Arenas. 2016. “The Physics of Spreading Processes in Multilayer Networks.” Nature Physics 12 (10): 901–6.
Deng, Haowen, Tolga Birdal, and Slobodan Ilic. 2018. “PPFNet: Global Context Aware Local Features for Robust 3D Point Matching.” In Cvpr, 195–205.
Deng, Songgaojun, Shusen Wang, Huzefa Rangwala, Lijing Wang, and Yue Ning. 2020. “Cola-GNN: Cross-Location Attention Based Graph Neural Networks for Long-Term ILI Prediction.” In Proceedings of the 29th ACM International Conference on Information & Knowledge Management, 245–54.
Dey, Tamal K., and Yusu Wang. 2022a. Computational Topology for Data Analysis. Cambridge University Press.
Ebli, Stefania, Michaël Defferrard, and Gard Spreemann. 2020. “Simplicial Neural Networks.” NeurIPS Workshop on Topological Data Analysis and Beyond.
Edelsbrunner, Herbert, and John Harer. 2010. Computational Topology: An Introduction. American Mathematical Soc.
Efthymiou, Athanasios, Stevan Rudinac, Monika Kackovic, Marcel Worring, and Nachoem Wijnberg. 2021. “Graph Neural Networks for Knowledge Enhanced Visual Representation of Paintings.” arXiv Preprint arXiv:2105.08190.
Feng, Yifan, Haoxuan You, Zizhao Zhang, Rongrong Ji, and Yue Gao. 2019. “Hypergraph Neural Networks.” Proceedings of the AAAI Conference on Artificial Intelligence 33 (01): 3558–65.
Fey, Matthias, and Jan Eric Lenssen. 2019. “Fast Graph Representation Learning with PyTorch Geometric.” arXiv Preprint arXiv:1903.02428.
Gallicchio, Claudio, and Alessio Micheli. 2010. “Graph Echo State Networks.” In The 2010 International Joint Conference on Neural Networks (IJCNN), 1–8. IEEE.
Ghrist, Robert W. 2014. Elementary Applied Topology. Vol. 1. Createspace Seattle.
Giusti, Lorenzo, Claudio Battiloro, Lucia Testa, Paolo Di Lorenzo, Stefania Sardellitti, and Sergio Barbarossa. 2022. “Cell Attention Networks.” arXiv Preprint arXiv:2209.08179.
Goodfellow, Ian, Yoshua Bengio, Aaron Courville, and Yoshua Bengio. 2016. Deep Learning. Vol. 1. MIT Press Cambridge. https://mitpress.mit.edu/9780262035613/deep-learning/.
Hacker, Celia. 2020. “K-Simplex2vec: A Simplicial Extension of Node2vec.” NeurIPS Workshop on Topological Data Analysis and Beyond.
Hajij, Mustafa, Kyle Istvan, and Ghada Zamzmi. 2020. “Cell Complex Neural Networks.” In NeurIPS 2020 Workshop TDA and Beyond.
Hatcher, Allen. 2005. Algebraic Topology. Cambridge University Press.
Huang, Jiahui, Tolga Birdal, Zan Gojcic, Leonidas J Guibas, and Shi-Min Hu. 2022. “Multiway Non-Rigid Point Cloud Registration via Learned Functional Map Synchronization.” IEEE Transactions on Pattern Analysis and Machine Intelligence.
Jiang, Weiwei, and Jiayun Luo. 2022. “Graph Neural Network for Traffic Forecasting: A Survey.” Expert Systems with Applications, 117921.
Kipf, Thomas N., and Max Welling. 2016. “Semi-Supervised Classification with Graph Convolutional Networks.” arXiv Preprint arXiv:1609.02907.
Kokkinos, Iasonas, Michael M Bronstein, Roee Litman, and Alex M Bronstein. 2012. “Intrinsic Shape Context Descriptors for Deformable Shapes.” In Cvpr, 159–66. IEEE.
Krizhevsky, Alex, Ilya Sutskever, and Geoffrey E. Hinton. 2012. “ImageNet Classification with Deep Convolutional Neural Networks.” In Advances in Neural Information Processing Systems. https://papers.nips.cc/paper_files/paper/2012/hash/c399862d3b9d6b76c8436e924a68c45b-Abstract.html.
La Gatta, Valerio, Vincenzo Moscato, Mirko Pennone, Marco Postiglione, and Giancarlo Sperlı́. 2022. “Music Recommendation via Hypergraph Embedding.” IEEE Transactions on Neural Networks and Learning Systems.
Lambiotte, Renaud, Martin Rosvall, and Ingo Scholtes. 2019. “From Networks to Optimal Higher-Order Models of Complex Systems.” Nature Physics 15 (4): 313–20.
LeCun, Yann, Léon Bottou, Yoshua Bengio, and Patrick Haffner. 1998. “Gradient-Based Learning Applied to Document Recognition.” Proceedings of the IEEE 86 (11): 2278–2324. https://ieeexplore.ieee.org/document/726791.
Loukas, Andreas. 2019. “What Graph Neural Networks Cannot Learn: Depth Vs Width.” arXiv Preprint arXiv:1907.03199.
Love, Ephy R., Benjamin Filippenko, Vasileios Maroulas, and Gunnar Carlsson. 2023a. “Topological Convolutional Layers for Deep Learning.” Jmlr 24 (59): 1–35.
Masci, Jonathan, Davide Boscaini, Michael Bronstein, and Pierre Vandergheynst. 2015. “Geodesic Convolutional Neural Networks on Riemannian Manifolds.” In Conference on Computer Vision and Pattern Recognition.
Monti, Federico, Davide Boscaini, Jonathan Masci, Emanuele Rodola, Jan Svoboda, and Michael M. Bronstein. 2017. “Geometric Deep Learning on Graphs and Manifolds Using Mixture Model CNNs.” In Cvpr, 5115–24.
Morris, Christopher, Martin Ritzert, Matthias Fey, William L. Hamilton, Jan Eric Lenssen, Gaurav Rattan, and Martin Grohe. 2019. “Weisfeiler and Leman Go Neural: Higher-Order Graph Neural Networks.” In Proceedings of the AAAI Conference on Artificial Intelligence.
Murgas, Kevin A., Emil Saucan, and Romeil Sandhu. 2022. “Hypergraph Geometry Reflects Higher-Order Dynamics in Protein Interaction Networks.” Scientific Reports 12 (1): 20879.
Oballe, Christopher, Alan Cherne, Dave Boothe, Scott Kerick, Piotr J Franaszczuk, and Vasileios Maroulas. 2021. “Bayesian Topological Signal Processing.” Discrete & Continuous Dynamical Systems-S.
Qi, Charles R., Hao Su, Kaichun Mo, and Leonidas J. Guibas. 2017. “PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation.” In Cvpr, 652–60.
Rempe, Davis, Tolga Birdal, Yongheng Zhao, Zan Gojcic, Srinath Sridhar, and Leonidas J Guibas. 2020. “CASPR: Learning Canonical Spatiotemporal Point Cloud Representations.” Neurips 33: 13688–701.
Robinson, Michael. 2014. Topological Signal Processing. Vol. 81. Springer.
Roddenberry, T. Mitchell, Nicholas Glaze, and Santiago Segarra. 2021. “Principled Simplicial Neural Networks for Trajectory Prediction.” In International Conference on Machine Learning.
Roddenberry, T. Mitchell, Michael T. Schaub, and Mustafa Hajij. 2022. “Signal Processing on Cell Complexes.” In IEEE International Conference on Acoustics, Speech and Signal Processing.
Rombach, Robin, Andreas Blattmann, Dominik Lorenz, Patrick Esser, and Björn Ommer. 2022. “High-Resolution Image Synthesis with Latent Diffusion Models.” In Computer Vision and Pattern Recognition. https://www.computer.org/csdl/proceedings-article/cvpr/2022/694600k0674/1H1iFsO7Zuw.
Sardellitti, Stefania, and Sergio Barbarossa. 2022. “Topological Signal Representation and Processing over Cell Complexes.” arXiv Preprint arXiv:2201.08993.
Scarselli, Franco, Marco Gori, Ah Chung Tsoi, Markus Hagenbuchner, and Gabriele Monfardini. 2008. “The Graph Neural Network Model.” IEEE Transactions on Neural Networks 20 (1): 61–80.
Schaub, Michael T., Austin R. Benson, Paul Horn, Gabor Lippner, and Ali Jadbabaie. 2020. “Random Walks on Simplicial Complexes and the Normalized Hodge 1-Laplacian.” SIAM Review 62 (2): 353–91.
Schaub, Michael T., Jean-Baptiste Seby, Florian Frantzen, T. Mitchell Roddenberry, Yu Zhu, and Santiago Segarra. 2022. “Signal Processing on Simplicial Complexes.” In Higher-Order Systems, 301–28. Springer.
Schaub, Michael T., and Santiago Segarra. 2018. “Flow Smoothing and Denoising: Graph Signal Processing in the Edge-Space.” In 2018 IEEE Global Conference on Signal and Information Processing (GlobalSIP), 735–39.
Schaub, Michael T., Yu Zhu, Jean-Baptiste Seby, T. Mitchell Roddenberry, and Santiago Segarra. 2021. “Signal Processing on Higher-Order Networks: Livin’on the Edge... And Beyond.” Signal Processing 187: 108149.
Schiff, Yair, Vijil Chenthamarakshan, Karthikeyan Natesan Ramamurthy, and Payel Das. 2020. “Characterizing the Latent Space of Molecular Deep Generative Models with Persistent Homology Metrics.” arXiv Preprint arXiv:2010.08548.
Shuman, David I., Benjamin Ricaud, and Pierre Vandergheynst. 2016. “Vertex-Frequency Analysis on Graphs.” Applied and Computational Harmonic Analysis 40 (2): 260–91.
Simonyan, Karen, and Andrew Zisserman. 2014. “Very Deep Convolutional Networks for Large-Scale Image Recognition.” arXiv Preprint arXiv:1409.1556. https://arxiv.org/abs/1409.1556.
Singh, Gurjeet, Facundo Mémoli, Gunnar E Carlsson, et al. 2007. “Topological Methods for the Analysis of High Dimensional Data Sets and 3d Object Recognition.” PBG@ Eurographics 2: 091–100.
Skardal, Per Sebastian, Lluı́s Arola-Fernández, Dane Taylor, and Alex Arenas. 2021. “Higher-Order Interactions Improve Optimal Collective Dynamics on Networks.” arXiv Preprint arXiv:2108.08190.
Sutskever, Ilya, Oriol Vinyals, and Quoc V. Le. 2014. “Sequence to Sequence Learning with Neural Networks.” In Advances in Neural Information Processing Systems. https://arxiv.org/abs/1409.3215.
Torres, Leo, Ann S Blevins, Danielle Bassett, and Tina Eliassi-Rad. 2021. “The Why, How, and When of Representations for Complex Systems.” SIAM Review 63 (3): 435–85.
Vaswani, Ashish, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. 2017. “Attention Is All You Need.” https://papers.nips.cc/paper_files/paper/2017/hash/3f5ee243547dee91fbd053c1c4a845aa-Abstract.html.
Wu, Zhirong, Shuran Song, Aditya Khosla, Fisher Yu, Linguang Zhang, Xiaoou Tang, and Jianxiong Xiao. 2015. “3D ShapeNets: A Deep Representation for Volumetric Shapes.” In Cvpr, 1912–20.
Wu, Zonghan, Shirui Pan, Fengwen Chen, Guodong Long, Chengqi Zhang, and S Yu Philip. 2020. “A Comprehensive Survey on Graph Neural Networks.” IEEE Transactions on Neural Networks and Learning Systems 32 (1): 4–24.
Yang, Maosheng, and Elvin Isufi. 2023. “Convolutional Learning on Simplicial Complexes.” arXiv Preprint arXiv:2301.11163.
Yang, Maosheng, Elvin Isufi, Michael T Schaub, and Geert Leus. 2021. “Finite Impulse Response Filters for Simplicial Complexes.” In 2021 29th European Signal Processing Conference (EUSIPCO), 2005–9. IEEE.
Zhang, Shi-Xue, Xiaobin Zhu, Jie-Bo Hou, Chang Liu, Chun Yang, Hongfa Wang, and Xu-Cheng Yin. 2020. “Deep Relational Reasoning Graph Network for Arbitrary Shape Text Detection.” In Cvpr, 9699–9708.
Zhao, Yongheng, Guangchi Fang, Yulan Guo, Leonidas Guibas, Federico Tombari, and Tolga Birdal. 2022. “3DPointCaps++: Learning 3D Representations with Capsule Networks.” Ijcv 130 (9): 2321–36.
Zhou, Jie, Ganqu Cui, Shengding Hu, Zhengyan Zhang, Cheng Yang, Zhiyuan Liu, Lifeng Wang, Changcheng Li, and Maosong Sun. 2020. “Graph Neural Networks: A Review of Methods and Applications.” AI Open 1: 57–81.
Zhu, Jianming, Junlei Zhu, Smita Ghosh, Weili Wu, and Jing Yuan. 2018. “Social Influence Maximization in Hypergraph in Social Networks.” IEEE Transactions on Network Science and Engineering 6 (4): 801–11.

  1. All figures in this paper should be displayed in color, as different colors communicate different pieces of information.↩︎