E A mapper-induced topology-preserving CC-pooling operation
In this section, we give an example of constructing a shape-preserving pooling operation on a CC \(\mathcal{X}\). Specifically, we demonstrate the case in which \(\mathcal{X}\) is a graph, and utilize the mapper on graphs (MOG) construction (Hajij, Wang, and Rosen 2018), which is a graph skeletonization algorithm that can be used to augment \(\mathcal{X}\) with topology-preserving higher-rank cells, as demonstrated in Figure 2.3. Although we only demonstrate the shape-preserving pooling construction on graphs, the method suggested herein can be easily extended to CCs.
Let \(\mathcal{X}\) be a connected graph and \(g\colon\mathcal{X}^{0} \to [0,1]\) a scalar function. Let \(\mathcal{U}=\{U_\alpha\}_{\alpha \in I}\) be a finite collection of open sets that covers the interval \([0,1]\). The MOG construction of a graph \(MOG(V_{MOG},E_{MOG})\) based on the triplet (\(\mathcal{X}\), \(g\), \(\mathcal{U}\)) consists of the following steps:
- We first use the cover \(\mathcal{U}\) to construct the pull-back cover \(g^{\star}(\mathcal{U})=\{g^{-1}(U_{\alpha})\}_{\alpha \in I}\).
- The vertex set \(V_{MOG}\) is formed by considering the connected components (i.e., maximal connected subgraphs) induced by \(g^{-1}(U_\alpha)\) for each \(\alpha\).
- The edge set \(E_{MOG}\) is formed by considering the intersection among the connected components computed in step 2.
Figure E.1 shows an illustrative example of applying the MOG algorithm to a graph. Figure E.1(a) shows the graph on which the MOG algorithm is applied, while Figure E.1(b) visualizes the scalar function \(g\) and the covering \(\mathcal{U}\), which consists of four covering elements depicted in red, orange, yellow and blue colors.
![An illustration of the MOG algorithm. The input to the MOG algorithm is a triplet $(\mathcal{X}, g, \mathcal{U})$, where $\mathcal{X}$ is a graph, $g\colon\mathcal{X}^0\to [0,1]$ is a scalar function defined on the vertex set of $\mathcal{X}$, and $\mathcal{U}$ is a cover of $[0,1]$. (a): An input graph $\mathcal{X}$. (b): The scalar function $g\colon\mathcal{X}\to [0,1]$ is visualized by color-mapping its scalar values according to the displayed color bar. Figure (b) also shows the covering $\mathcal{U}= \{U_1,U_2, U_3, U_4\}$ depicted in red, orange, yellow and blue colors. (c): We pull back via $g$ each cover element $U_i$ in $\mathcal{U}$, and we compute the connected components in $g^{-1}(U_i)$. (d): The vertex set in the graph generated by the MOG algorithm consists of the connected components induced by $g^{-1}(U_i)$, while the edge set is formed by considering the intersection among the connected components. Note that the graph generated by the MOG algorithm approximates the shape of the input graph.](figures/graph_tda_appendix.png)
FIGURE E.1: An illustration of the MOG algorithm. The input to the MOG algorithm is a triplet \((\mathcal{X}, g, \mathcal{U})\), where \(\mathcal{X}\) is a graph, \(g\colon\mathcal{X}^0\to [0,1]\) is a scalar function defined on the vertex set of \(\mathcal{X}\), and \(\mathcal{U}\) is a cover of \([0,1]\). (a): An input graph \(\mathcal{X}\). (b): The scalar function \(g\colon\mathcal{X}\to [0,1]\) is visualized by color-mapping its scalar values according to the displayed color bar. Figure (b) also shows the covering \(\mathcal{U}= \{U_1,U_2, U_3, U_4\}\) depicted in red, orange, yellow and blue colors. (c): We pull back via \(g\) each cover element \(U_i\) in \(\mathcal{U}\), and we compute the connected components in \(g^{-1}(U_i)\). (d): The vertex set in the graph generated by the MOG algorithm consists of the connected components induced by \(g^{-1}(U_i)\), while the edge set is formed by considering the intersection among the connected components. Note that the graph generated by the MOG algorithm approximates the shape of the input graph.
The connected components obtained from the MOG algorithm can be used to augment a graph \(\mathcal{X}\) with a skeleton \(\mathcal{X}^2\) of dimension 2, thus constructing a CC, as described in Proposition B.1. We denote the resulting CC by \(\mathcal{X}_{g,\mathcal{U}}\). Figure E.2 demonstrates the construction of a CC using this augmentation process based on the MOG algorithm.
FIGURE E.2: A visual example of obtaining a CC from a graph via the MOG algorithm. (a): An input graph \(\mathcal{X}\). (b): The graph \(\mathcal{X}\) is augmented by the \(2\)-cells formed via the connected components obtained from applying the MOG algorithm to \(\mathcal{X}\). (c): The CC \(X_{g,\mathcal{U}}\) obtained by augmenting \(\mathcal{X}\) with these \(2\)-cells.
MOG is a topology-preserving graph skeletonization algorithm, which can be used to coarsen the size of an input graph \(\mathcal{X}\). Such coarsening typically occurs when constructing a pooling layer. So, the skeleton \(\mathcal{X}^2\) generated by the MOG algorithm can be utilized to obtain a feature-preserving pooling operation. Figure E.3 illustrates that the MOG algorithm coarsens an input graph to produce a graph that preserves topological features of the input graph.
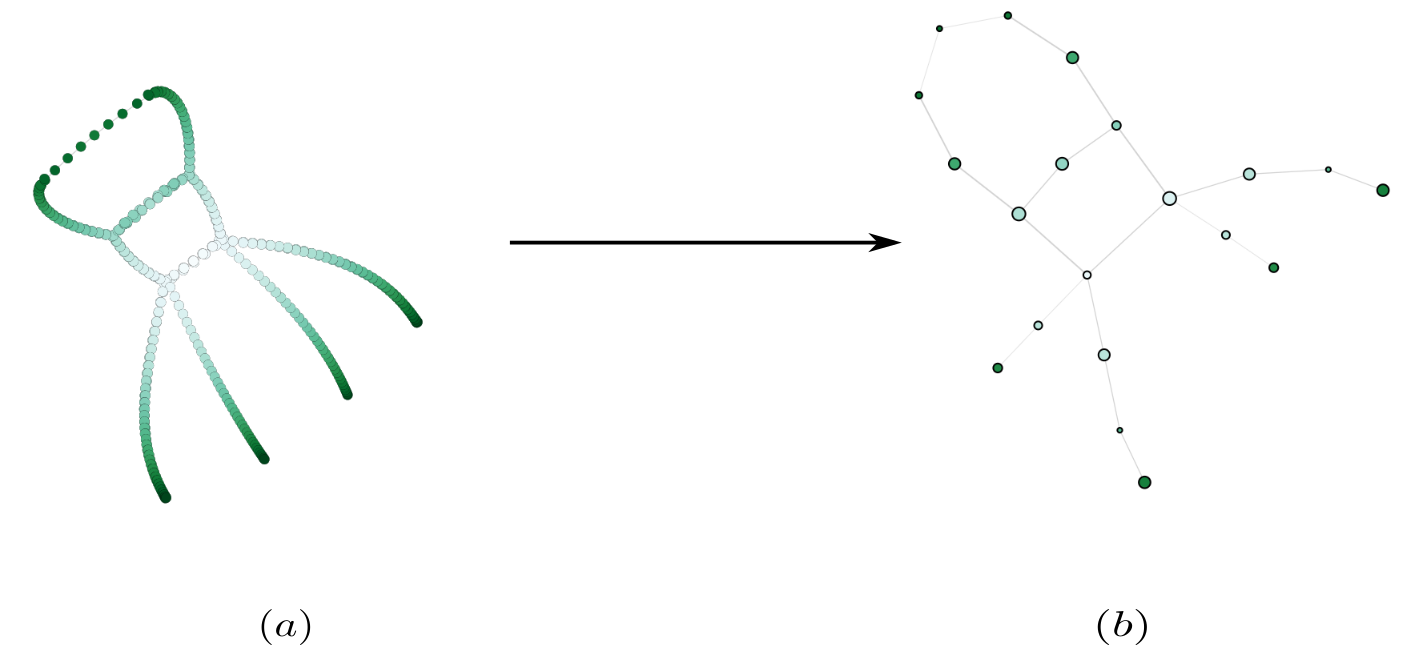
FIGURE E.3: Illustration of coarsening a graph via the MOG algorithm. (a): Visualization of a graph and of a scalar function defined on it, which are used as inputs to the MOG algorithm. The scalar function is visualized by color-mapping its scalar values. (b): The resulting MOG graph. Notice how the MOG construction preserves the overall shape of the original graph.
To recap, the MOG algorithm receives an input graph, and outputs a coarsened graph along with connected components. The connected components yield in turn a CC. The coarsened graph and the adjacency relation between the \(2\)-cells of the associated CC are related, as elaborated in Proposition E.1. Figure E.4 conveys visually Proposition E.1.
Proposition E.1 (MOG as a CC) Let \((\mathcal{X}, g, \mathcal{U})\) be a triplet consisting of a graph \(\mathcal{X}\), a scalar function \(g\colon\mathcal{X}^0\to [0,1]\) defined on the vertex set of \(\mathcal{X}\), and a cover \(\mathcal{U}\) of \([0,1]\). Let \(MOG(\mathcal{X}\), \(g\), \(\mathcal{U})\) be the graph generated by the MOG algorithm upon receiving the triplet \((\mathcal{X}, g, \mathcal{U})\) as input. Furthermore, let \(\mathcal{X}_{g,\mathcal{U}}\) be the CC constructed from the connected components that are generated by the MOG algorithm. The adjacency matrix of the graph \(MOG(\mathcal{X}\), \(g\), \(\mathcal{U})\) is equivalent to the adjacency matrix \(A_{2,2}\) of the CC \(\mathcal{X}_{g,\mathcal{U}}\).
Proof. The proof follows by observing that the \(2\)-cells, which are augmented to \(\mathcal{X}\) to generate the CC \(\mathcal{X}_{g,\mathcal{U}}\), are 2-adjacent if and only if they intersect on a vertex. Moreover, two cells intersect on a vertex if and only if there is an edge between them in the graph \(MOG(\mathcal{X}, g, \mathcal{U})\) outputted by the MOG algorithm.
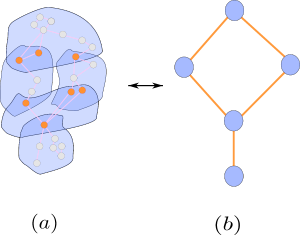
FIGURE E.4: Visual demonstration of how a MOG can be viewed as a CC. (a): Visualization of a CC \(\mathcal{X}_{g,\mathcal{U}},\) which highlights the intersection between blue 2-cells. (b): The corresponding \(MOG(\mathcal{X}, g, \mathcal{U})\) graph. There is a one-to-one correspondence between the blue 2-cells of \(\mathcal{X}_{g,\mathcal{U}}\) on the left-hand side and the blue vertices of \(MOG(\mathcal{X}, g, \mathcal{U})\) on the right-hand side. Further, two blue 2-cells of \(\mathcal{X}_{g,\mathcal{U}}\) (left) intersect on an orange vertex if and only if there is an orange edge (right) that connects the corresponding two vertices of \(MOG(\mathcal{X}, g, \mathcal{U})\).
Given a CC \(X_{g,\mathcal{U}}\) obtained from a graph \(\mathcal{X}\) via the MOG algorithm, the map \(B_{0,2}^T\colon\mathcal{C}^0(X_{g,\mathcal{U}})\to \mathcal{C}^2(X_{g,\mathcal{U}})\) can be used to induce a shape-preserving CC-pooling operation (Definition 7.1). More specifically, a signal \(\mathbf{H}_0\) supported on the vertices of \(\mathcal{X}\) can be push-forwarded and pooled to a signal \(\mathbf{H}_2\) supported on the 2-cells of \(X_{g,\mathcal{U}}\).